수학의 언어로 세상을 본다면 / 오구리 히로시

 

 

 

 

 

아버지가 딸에게 전하는 수학

 

 

 

 

 

제1장 불확실한 정보를 가지고 판단한다

ㆍ살다보면 결정적인 판단을 하거나 단정을 내려야 할 일이 생긴다. 학교에서는 해답이 하나인 문제만 시험에 나온다. 그러나 현실 사회에서는 정답이 없는 경우가 더 많다. 그뿐만 아니라 문제를 풀기 위한 재료가 제대로 갖추어져 있다고도 할 수 없다. 

 

 

제2장 기본원리로 되돌아가본다

 

ㆍ수학에서는 구체적인 사물에서 벗어나 실체가 없는 '숫자 그 자체'의 추상적 성질을 생각한다. 

 

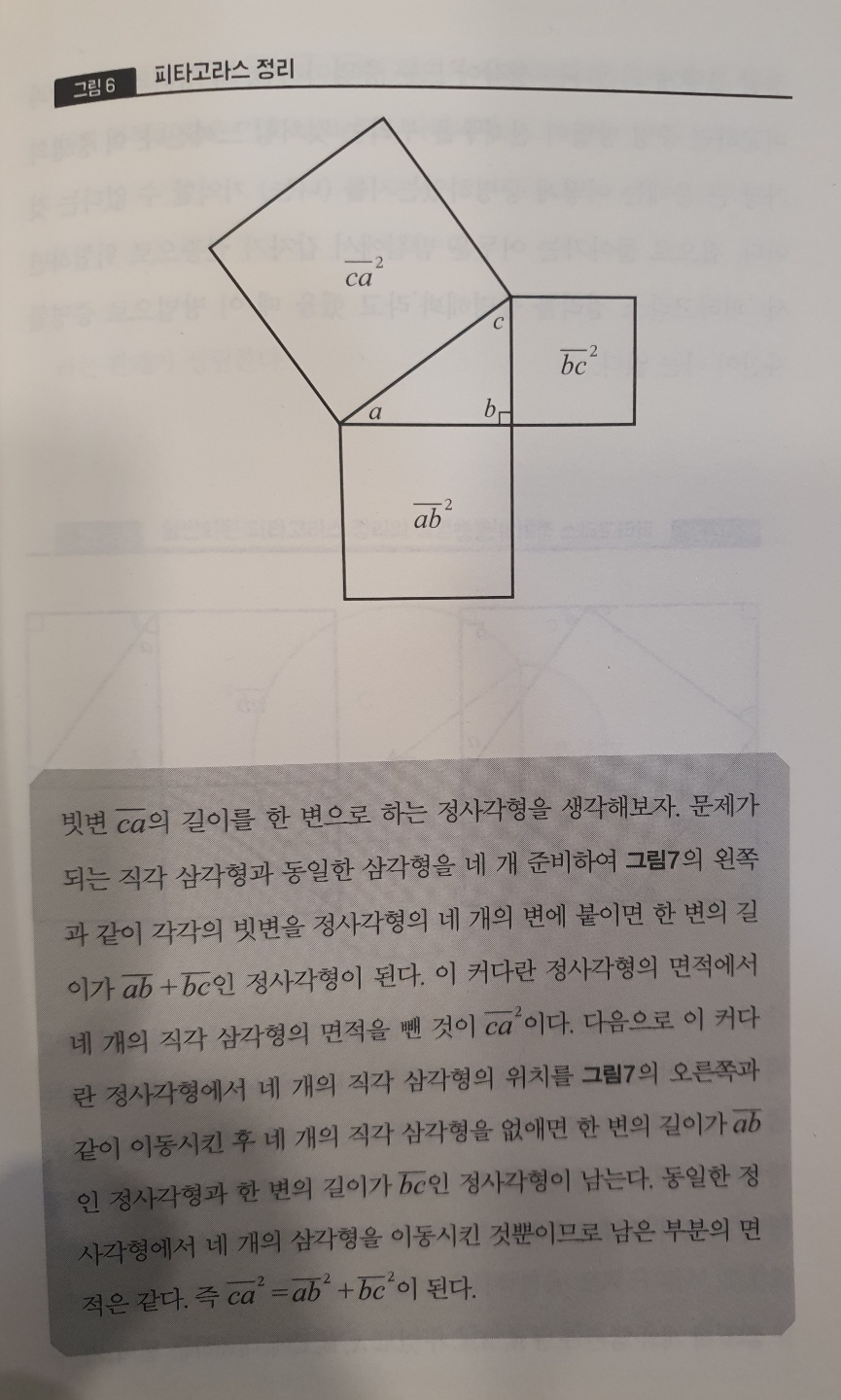
ㆍ음수와 음수의 곱셈에 대해서 생각해보자. 네가 매일 하교 길에 100원짜리 주스를 사마셨다고 하자. 이번에는 용돈이 없다고 한다. 저금이 매일 100원씩 줄어들 것이다. 하루가 지나면 100원, 이틀이 지나면 200원 줄어든다. n일이 지나면 100×n원 줄어든다. 이것을 (-100)×n으로 나타낼 수 있다. 여기서 하루 전의 경우, n=-1이라고 한다면 어떨까. 매일 100원짜리 주스를 사서 마셨기 때문에 100원씩 저금이 줄어드는 것이니 어제는 오늘보다 100원 더 많은 저금이 있었을 것이다. 즉 (-100)×(-1)=100이어야 한다. 그저께 즉 n=-2에는 200원 많았을 것이므로 (-100)×(-2)=200이 된다. 음수와 음수를 곱하면 양수가 된다고 예상할 수 있다.

 

 

제3장 큰 수도 무섭지 않다

 

ㆍ1945년 7월, 미국 뉴멕시코 주의 트리니티 실험장에서 세계 최초의 원자폭탄실험이 행해졌다. 그 3년 전에 시카고 대학에서 원자로를 건설하여 원자핵 분열의 지속적인 연쇄반응을 가능하게 한 엔리코 페르미도 맨해튼 계획의 일원으로 실험에 참가했다. 폭발하고 40초 후 관측기지에도 폭풍이 도달했다. 폭발이 있었던 지점을 바라보고 있던 페르미는 일어서서 머리 위로 두 손을 번쩍 들었다. 손에는 미리 준비해둔 메모용지가 있었다. 폭풍이 도달하자 양손을 펼쳤다. 종이쪽지는 2미터 반 정도 날아서 지면에 떨어졌다. 이것을 본 페르미는 잠시 생각한 후 참가자들을 보고 말했다. “TNT 화약 2만 톤에 상당하는 위력이군요.”

 

ㆍ칼로리는 에너지의 단위다. 

제4장 소수의 불가사의

ㆍ소수가 무한개 있다는 것을 알았는데, 소수를 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43… 이렇게 나열해보면 거기에는 어떤 패턴이 있지 않을까? 이 문제는 고대 그리스시대부터 현대에 이르기까지 수학자를 매료시켰다. 소수의 패턴을 찾는 것은 원자의 주기율표를 찾는 것과 같다고 생각한다. 19세기 화학자 드미트리 멘델레예프가 그때까지 발견된 원소를 원자량 순으로 나열하자, 그 성질에 주기적 패턴이 있다는 것을 알았다. 그 주기성을 가지고 새로운 원자의 존재를 예언했다. 그리고 멘델레예프의 주기율표는 20세기의 원자구조의 해명에 큰 영향을 미쳤다. 이와 마찬가지로 수의 아톰인 소수의 패턴을 이해하면, 수의 비밀을 보다 깊이 해명할 수 있다고 기대할 수 있다.

 

제5장 무한세계와 불완전성 정리

ㆍ1=0.99999…를 이해할 수 없다면 이 두 숫자의 차이는 무엇인가. 제2장에서 본 것처럼 덧셈과 뺄셈의 기본 규칙을 적용하면 a-b=0이라면 a=b가 된다. 그러므로 1-0.99999…=0이라고 하면 1=0.99999…도 인정하지 않을 수 없다. 그럼 1-0.99999…가 0이 아니라면 어떨까? 그때는 1과 0.99999…의 차이는 도대체 무엇인가가 문제가 된다.
생각해보면 0.99999…라는 무한 소수의 표기는 어쩐지 꺼림칙하다. 원래 ‘…’에는 무엇이 들어가는 것일까? 유한한 존재인 우리에게는 무한한 숫자가 늘어서 있는 무한 소수를 단번에 이해할 수 없다. 그래서 우리가 이해할 수 있는 0.9, 0.99, 0.999, 0.9999라는 유한 소수의 열을 생각해보자. 이처럼 숫자가 늘어서 있는 것을 ‘수열’이라고 한다. 이 수열과 1과의 차이를 계산해 보면 다음과 같다.

 

 

 

제6장 우주의 형태를 측정하다

 

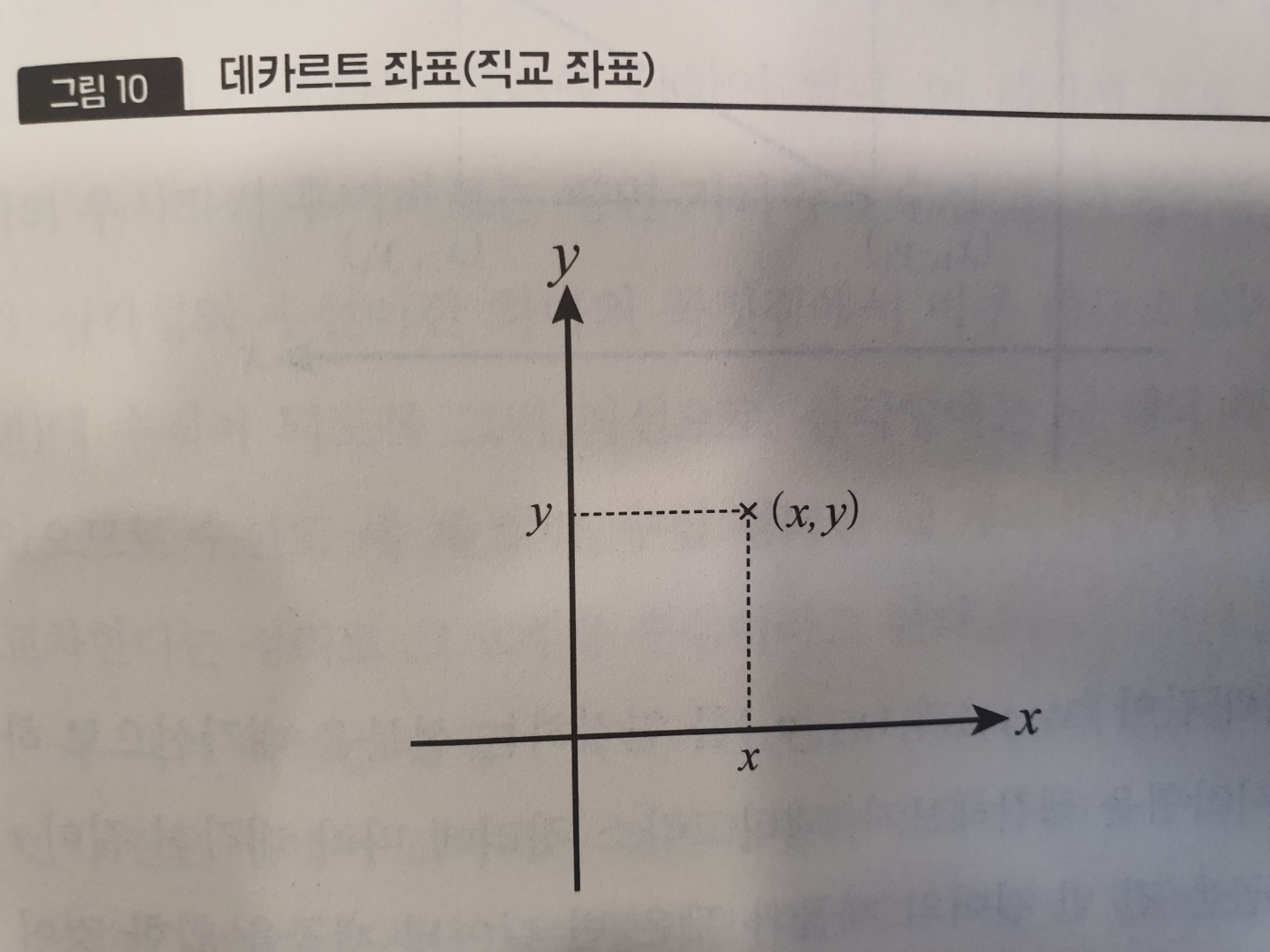
ㆍ좌표는 데카르트의 획기적인 아이디어이다. 

 

제7장 미적분은 적분부터

 

 

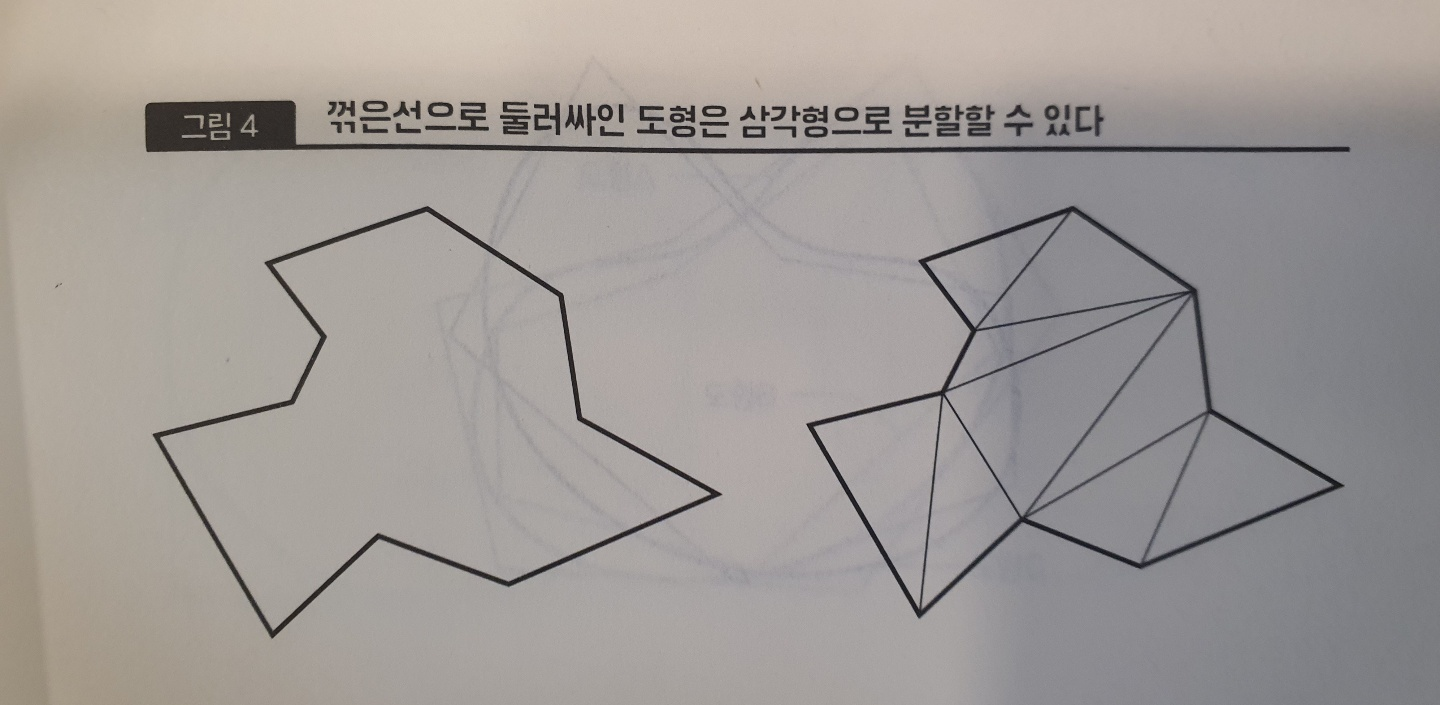
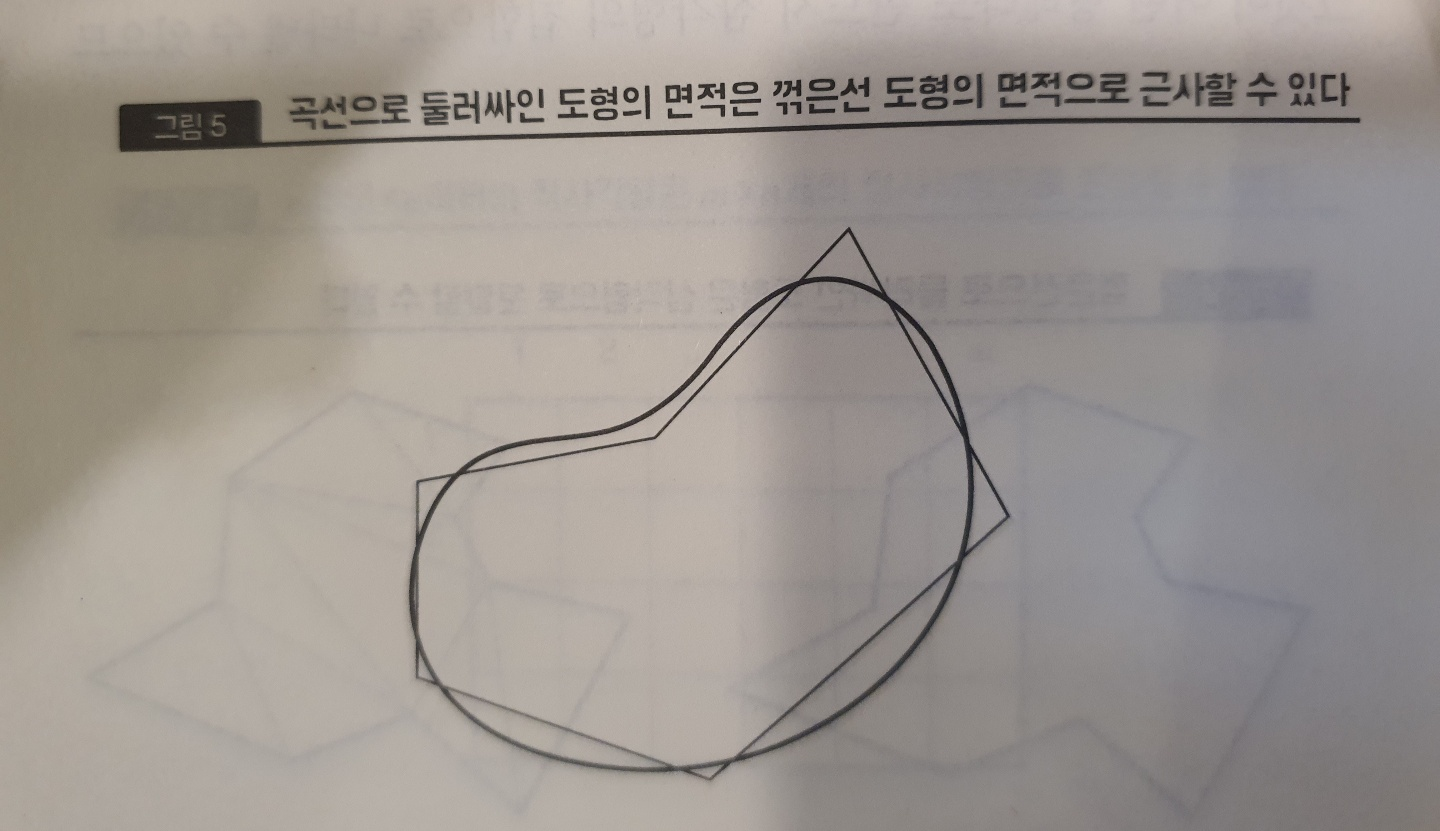
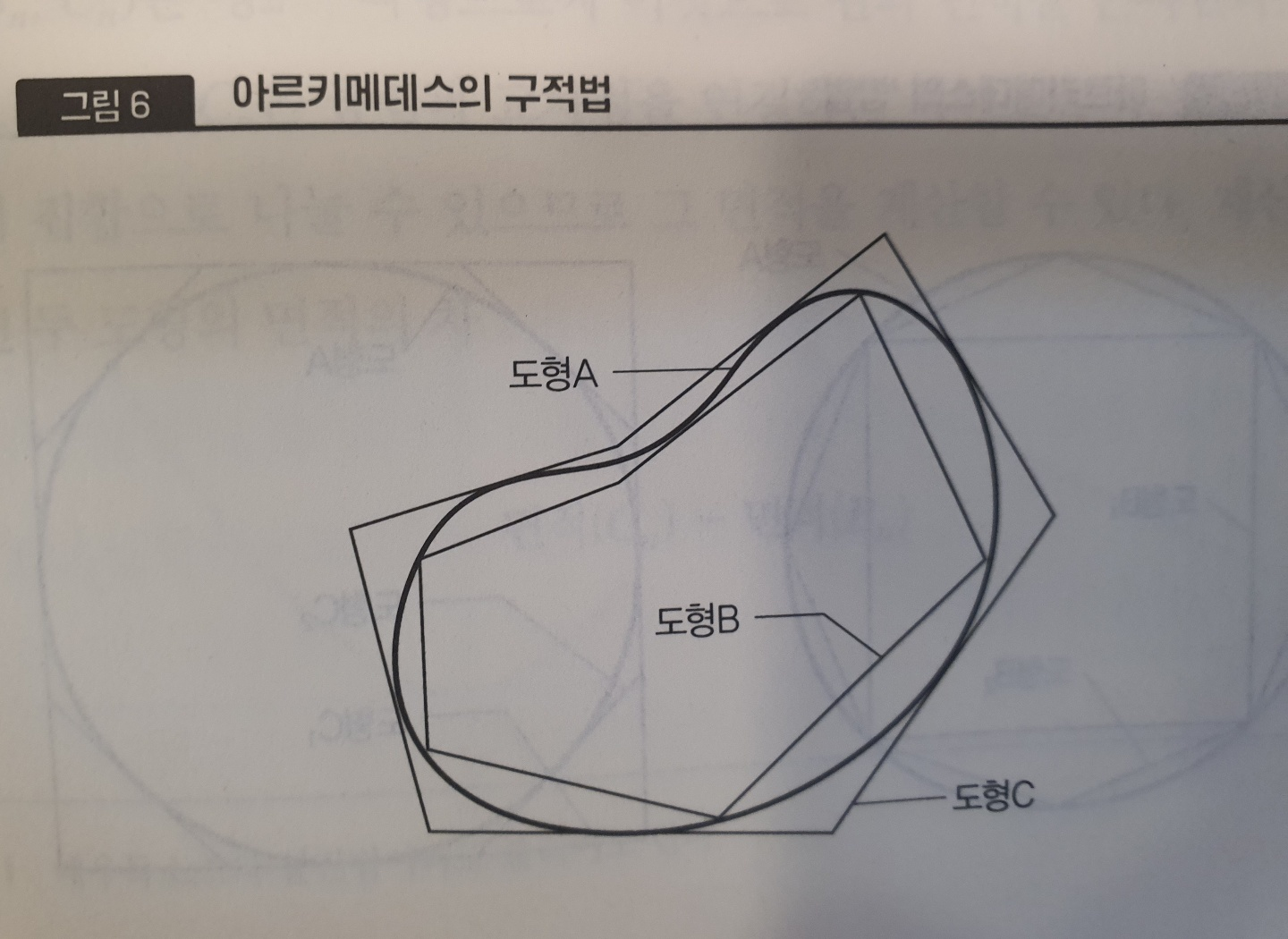
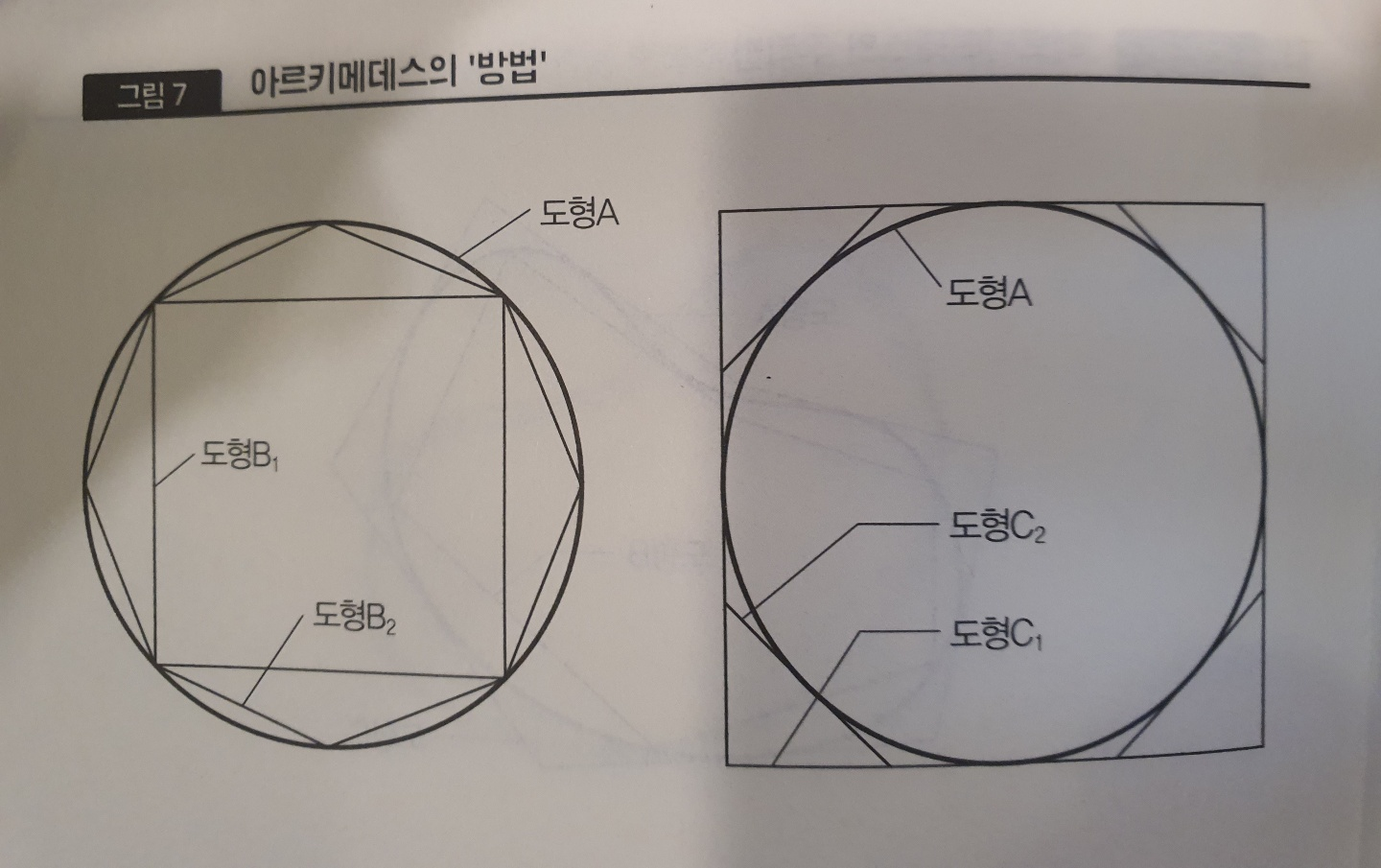
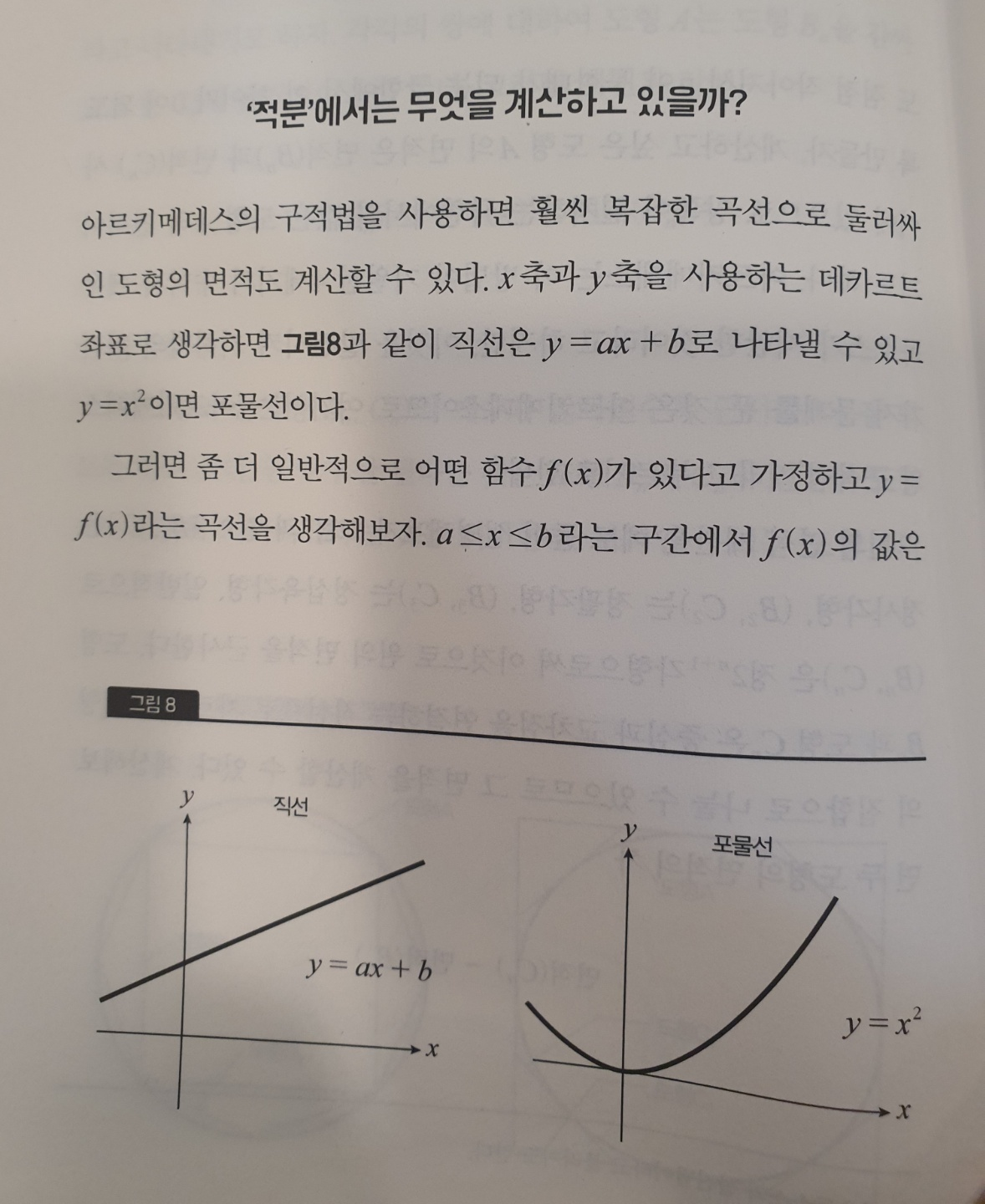
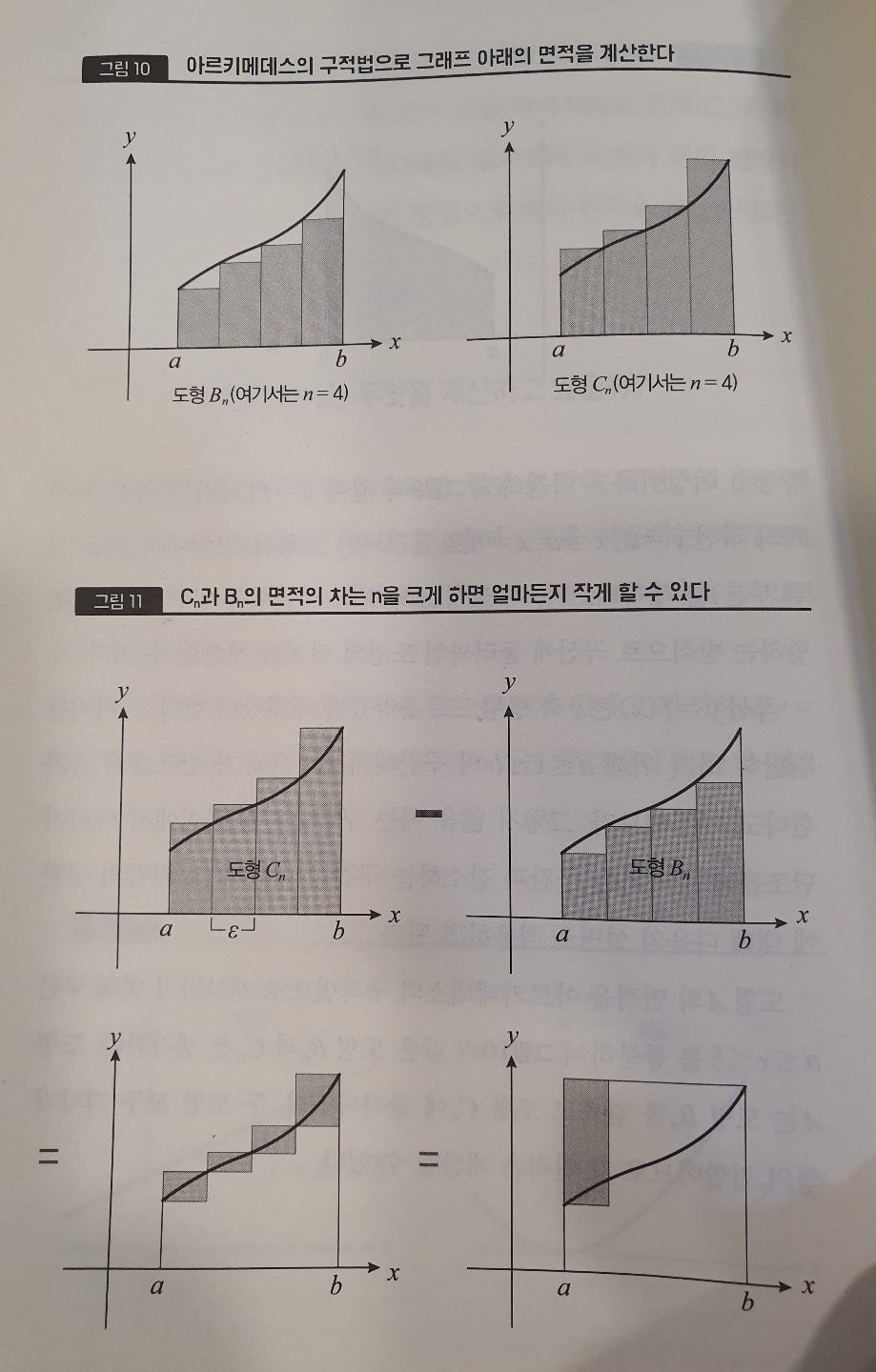
ㆍ고등학교 수학에서는 거의 모든 교과서가 미분을 먼저 설명한 후에 그 역연산으로서 부정적분을 도입한다. 그리고 면적을 계산하기 위한 정적분은 부정적분의 차이로서 정의한다. 이러한 순서는 완성된 수학을 논리적으로 가르친다는 의미에서는 이치에 맞지만, 역사적인 발전 순서로 보면 정반대이다. 아르키메데스가 면적을 계산하기 위해 적분을 연구한 것은 기원전 3세기이고 뉴턴과 라이프니츠가 미분법을 고안해낸 것은 17세기. 두 시기 사이에는 1800년 이상이나 차이가 있다. 역사적으로 적분이 먼저 발견된 것에는 이유가 있다. 적분은 면적이나 체적 등 눈에 보이는 양을 계산하는 데 직접 관계가 있다. 반면, 미분의 경우에는 무한 소수나 극한 등의 개념을 확실하게 이해할 필요가 있다. 예를 들면 운동하는 물체의 속도는 미분으로 정의할 수 있지만, 고대 그리스 시대에는 극한의 개념이 아직 확립되지 않았기 때문에 나중에 이야기하는 ‘날아가고 있는 화살은 멈춰 있다’라는 제논의 역설이 문제가 되었다. 미분은 수학적으로 더 ‘고상’한 개념이다. 

 

 

 

 

제8장 정말로 존재하는 ‘공상의 수’

 

 

 

제9장 ‘어려움’과 ‘아름다움’을 측정한다