법칙, 정리, 공식은 왜 만들어졌을까?
ㆍ주변의 다양한 현상을 심플하게 정의내려서 실생활에 적용하거나 다른 분야에 응용해 새로운 지식을 얻을 수 있도록 돕는 것이 바로 법칙-공식-정리다. 이를 잘 알고 있으면 자연계 또는 사회에서 일어나는 일을 한눈에 이해할 수 있게 된다. 결국 법칙은 인간의 지혜를 높이는 도구인 셈이다.
ㆍ법칙은 대상을 객관적으로 분석해 일정 조건에서 반드시 그렇게 되는 보편적인 관계성을 나타낸 것이다.
ㆍ정리란 수학적으로 참이라고 증명된 명제를 의미한다.
ㆍ공리는 증명이나 설명 없이 있는 그대로 자명한 명제를 의미한다. "평행한 두 선은 절대 만나지 않는다."
ㆍ역설은 추론과 현실 사이에 모순이다.
ㆍ16세기에 들어서면서 수량적인 데이터에서 귀납적으로 규칙성
ㆍ고대 이집트에서는 동쪽 지평선에서 별 시리우스가 태양보다 아주 약간 일찍 떠오르는 날을 기준으로 1년이 시작됐다. 이것을 ‘신출(Heliacal rising)’이라고 부르는데, 이 시기는 하지(夏至) 무렵이면서 이집트의 농지를 기름진 평야로 만들어 주는 나일강의 범람이 시작되는 때이기도 했다. 시리우스는 큰개자리의 알파성(가장 밝은 별)인 동시에 마이너스 1.5등성으로, 하늘 전체에서 가장 밝은 항성(천구에 붙박혀 있어서 별자리를 기준으로 거의 움직이지 않으며, 점 같이 보이는 천체)이다. 그런데 당시의 이집트 사람들은 시리우스가 동쪽 하늘에서 태양과 거의 비슷하게 떠오르는 시기를 어떻게 알았을까? 바로 별의 움직임을 자세히 관찰했기 때문이다. 밤하늘에 보이는 별의 방위는 계절에 따라 달라지는데, 이를 자세히 관찰하면 변화 속에서 일정한 규칙을 발견할 수 있다. 이처럼 어떤 현상을 관찰함으로써 규칙성이 발견되고, 그 규칙성이 일반성을 지님이 증명됨에 따라 ‘법칙’이 만들어졌다.
ㆍ현재의 우주론에 따르면 우주가 약 150억 년 전의 빅뱅 이후 지속적으로 팽창하고 있음은 분명하다. 그러나 아인슈타인이 일반 상대성 이론을 발표했을 당시는 우주가 변하지 않는 공간으로 여겨지던 시절이었다. 그런데 아인슈타인의 이론에서는 우주가 팽창하고 있거나 혹은 수축하고 있거나 둘 중 하나라는 결론이 나왔다. 아인슈타인은 이것이 이상하다고 생각해, 우주가 팽창도 수축도 하지 않는 정상 우주가 되도록 우주항이라는 새로운 항을 넣은 방정식을 제시했다.
그런데 1922년에 러시아의 물리학자인 알렉산드르 프리드만이 우주가 팽창할 가능성을 지적했고, 1929년에 에드윈 허블이 우주는 팽창하고 있다는 사실을 발견했다. 이를 두고 아인슈타인은 방정식에 우주항을 넣은 것을 “생애 최대의 실수였다”라고 말하며 후회했다고 한다.
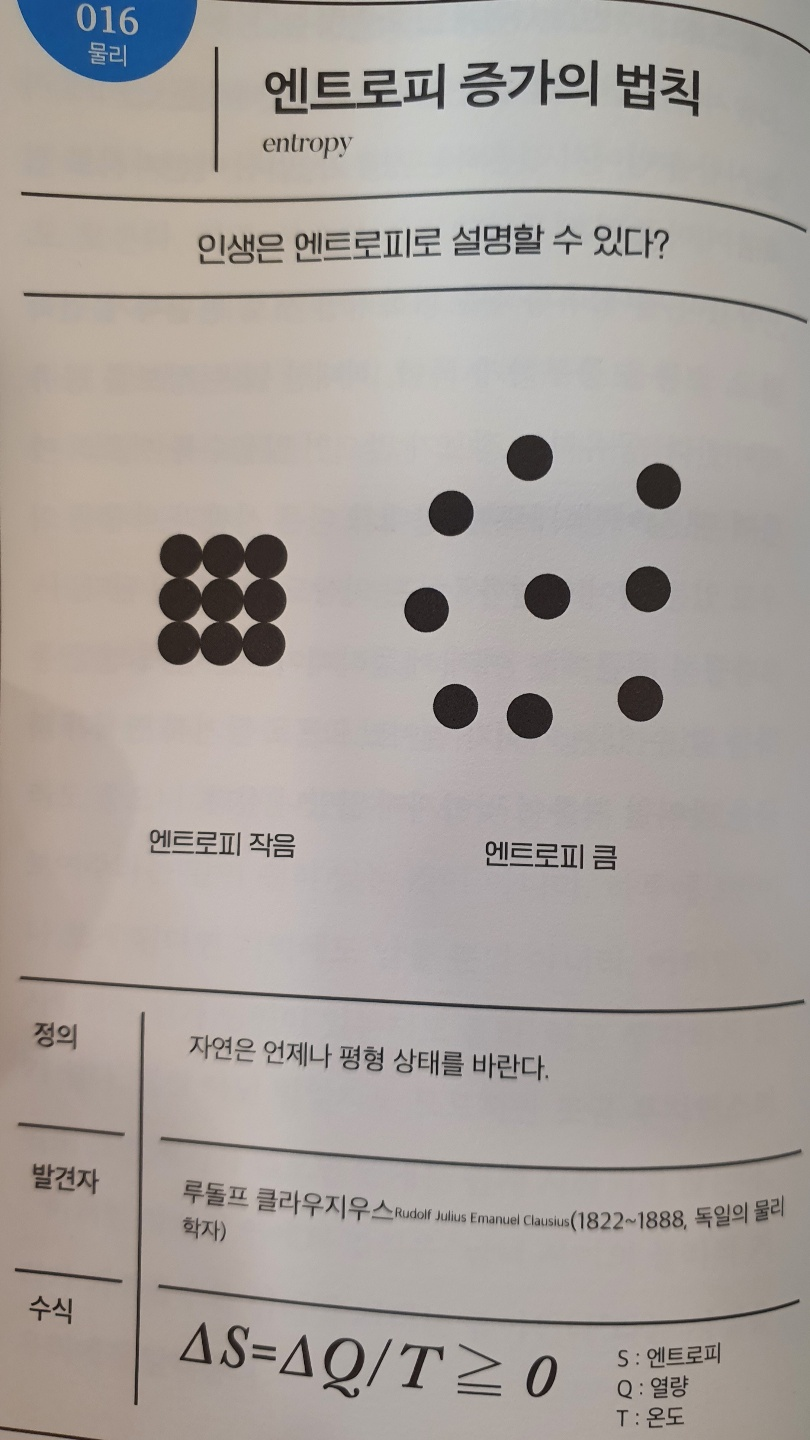
ㆍ애초에 생물이 이 세계에 존재하는 것은 방대한 양의 다양한 원자를 부자연스럽게 집중시킨 뒤, 그곳에서 에너지를 흡수해 소비했기 때문이다. 그러나 죽으면 다시 원자로 돌아가버리며, 이때가 엔트로피 최대의 상태이자 궁극의 평형 상태가 된다. 좀 더 쉬운 예를 들면 방은 아무리 치우고 정리해도 시간이 지남에 따라 결국 다시 어질러진다. 이것도 엔트로피 증가의 법칙에 따른 결과라 할 수 있다.
ㆍ피겨스케이팅을 즐기는 방법은 그 밖에도 또 있다. 회전의 메커니즘을 살펴보는 것이다. 경기를 잘 지켜보면 두 팔을 벌려서 회전할 때는 속도가 느리고, 두 팔을 오므려서 회전할 때는 속도가 빠르다는 사실을 알게 된다. 어째서일까? 직선 운동을 하고 있는 물체가 운동량을 가지듯이, 중심축의 주위를 회전하고 있는 물체에도 운동량이 발생한다. 이것을 각운동량이라고 한다. 각운동량은 각속도(회전 운동을 하는 물체가 단위 시간에 움직이는 각도)와 물체의 관성 모멘트를 곱한 값으로 표현된다. 관성 모멘트는 회전 운동에 대한 관성의 크기를 나타내는 것으로, 이 값이 클수록 회전 운동에 변화가 잘 일어나지 않게 된다.
Part. 1
No.001 AIDMA의 법칙
No.002 악마의 증명
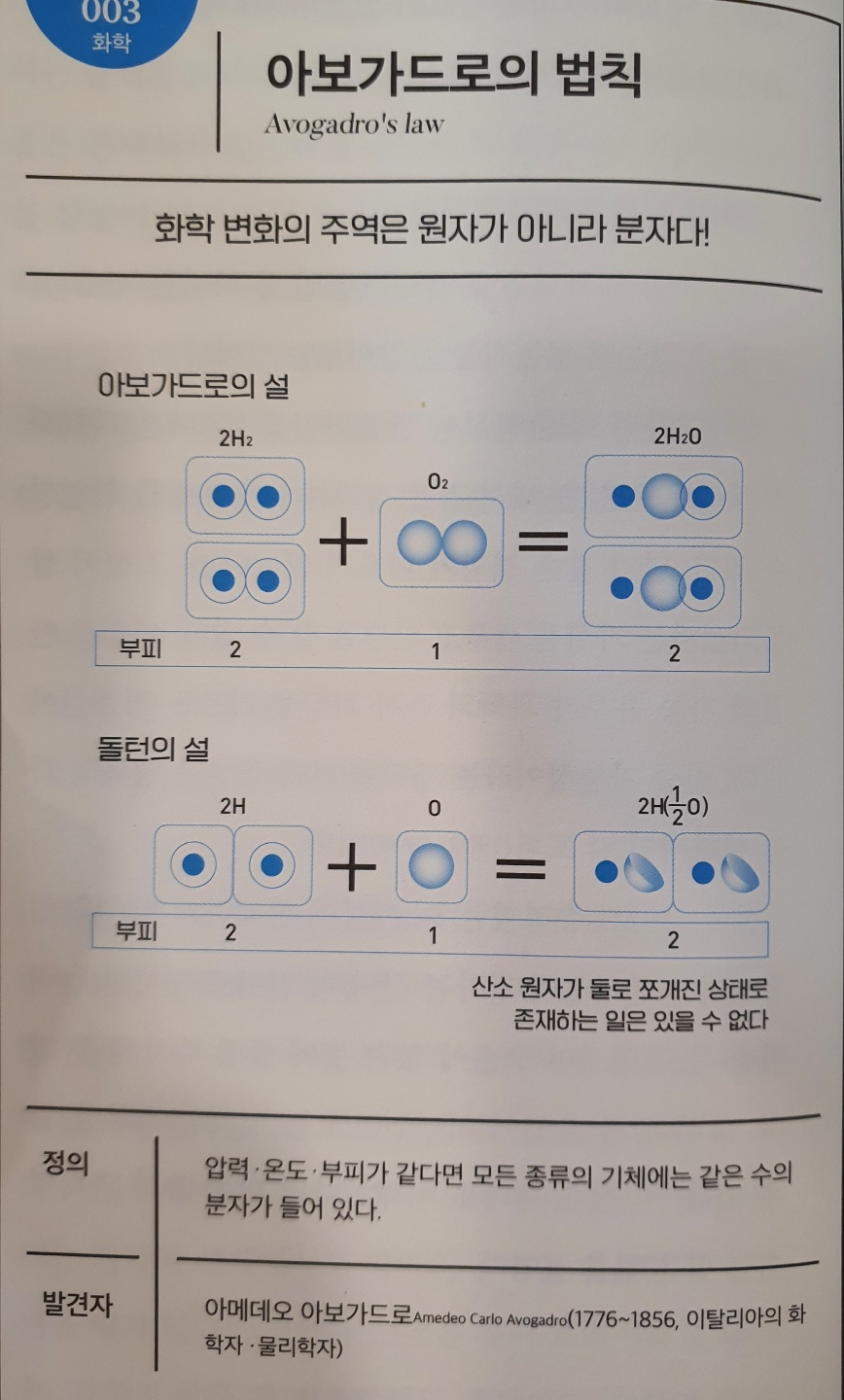
No.003 아보가드로의 법칙
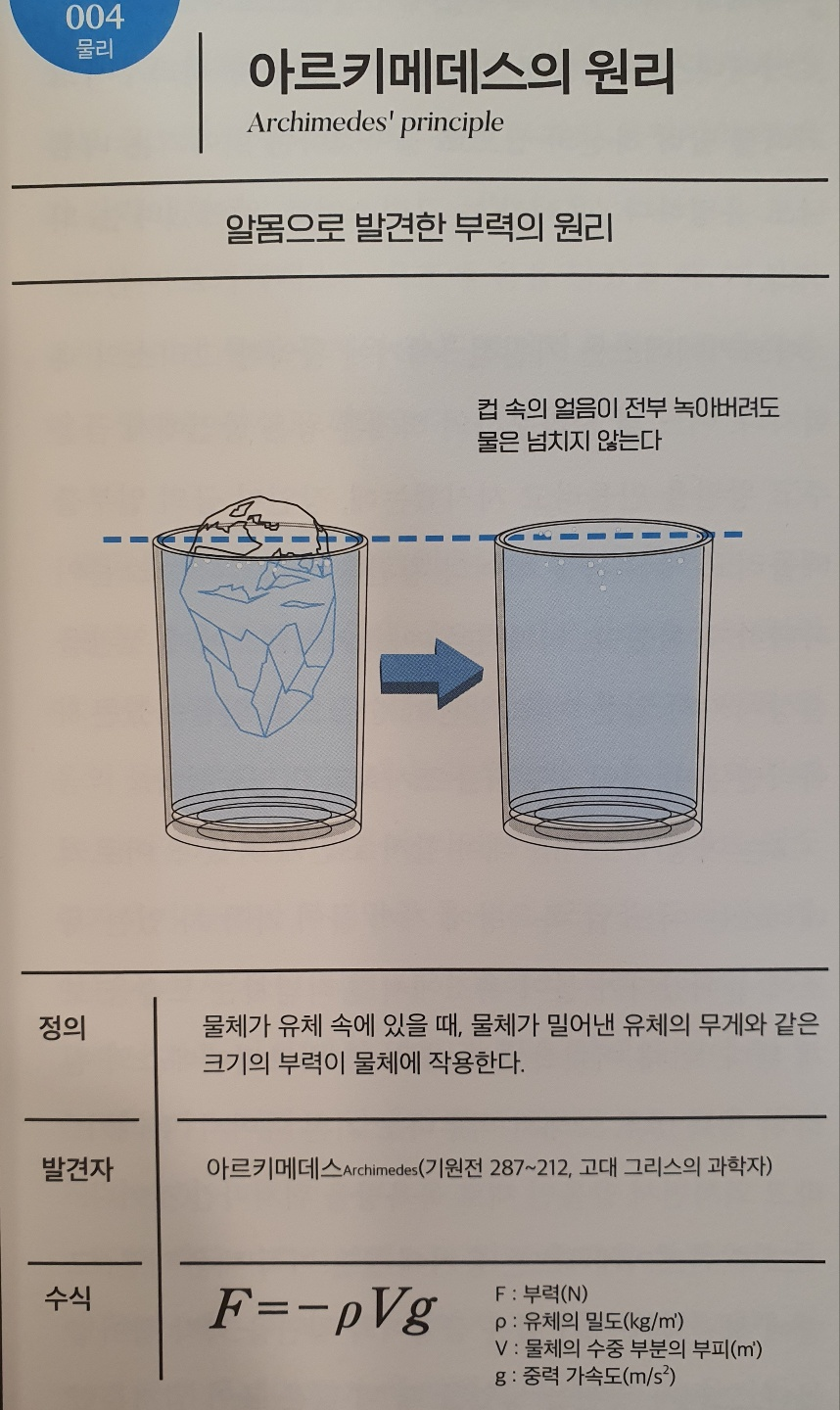
No.004 아르키메데스의 원리
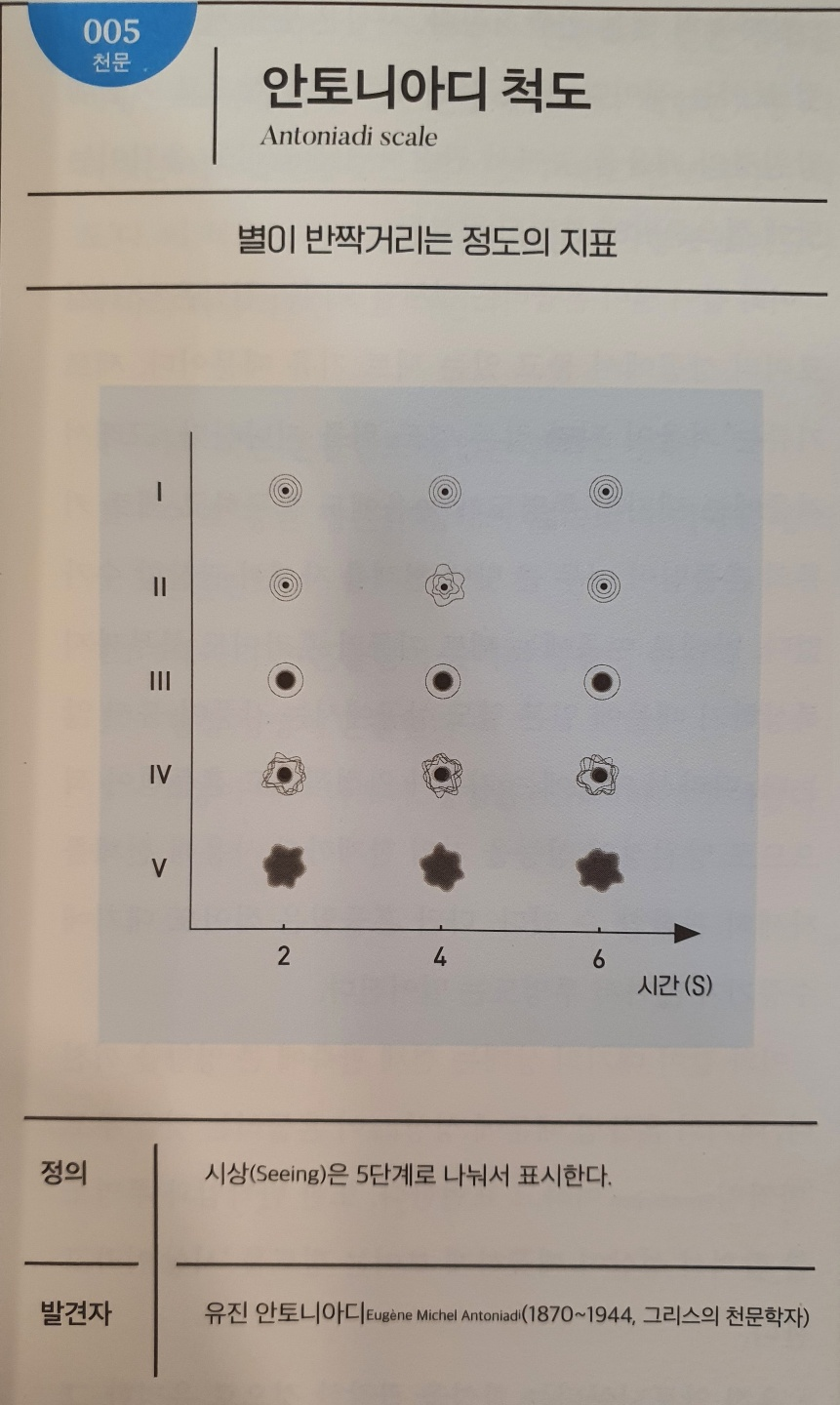
No.005 안토니아디 척도
No.006 앙페르의 법칙
No.007 EPR 역설
No.008 일반 상대성 이론
No.009 이노베이션의 딜레마
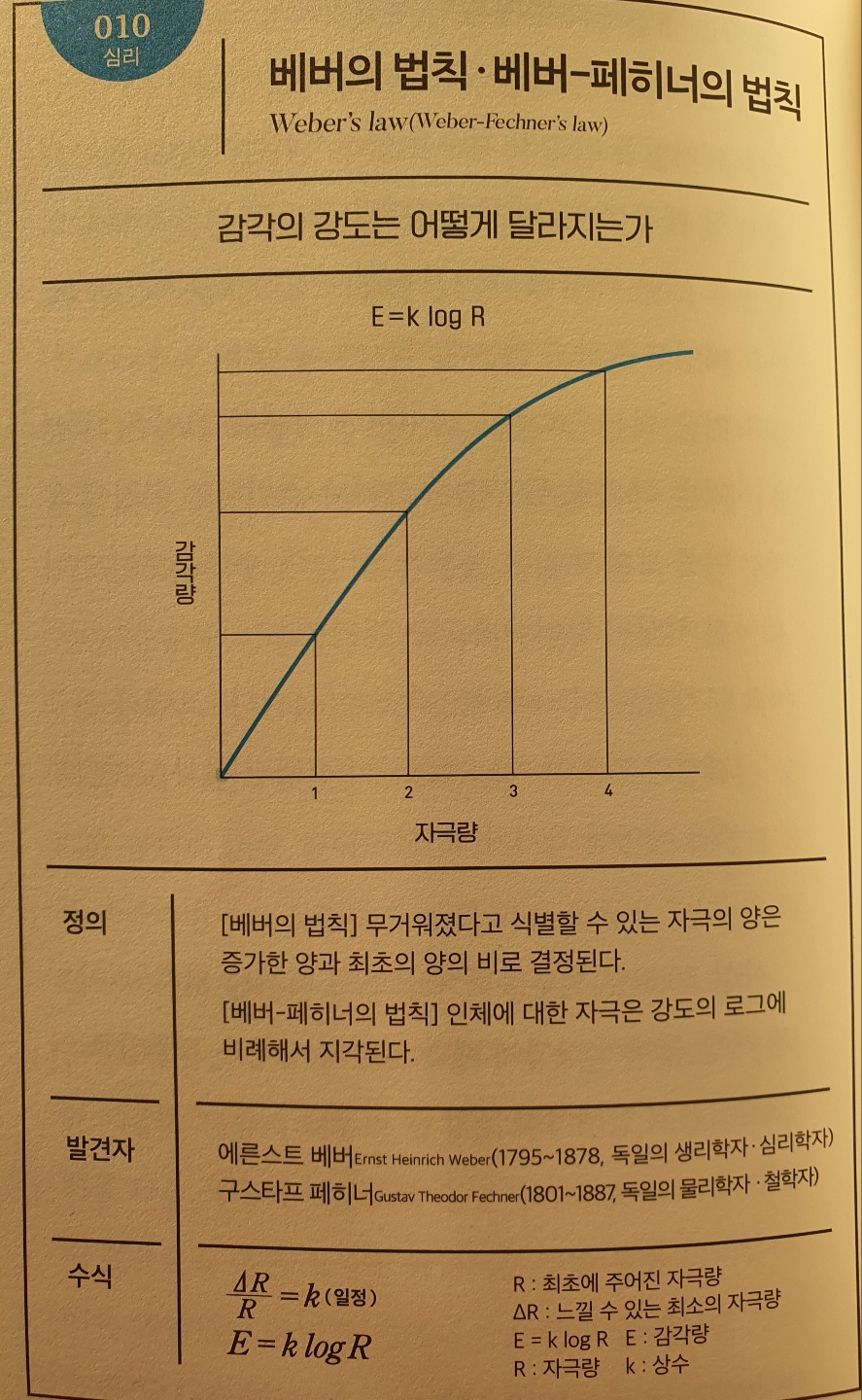
No.010 베버의 법칙·베버-페히너의 법칙
No.011 운동의 법칙(운동의 제2법칙)
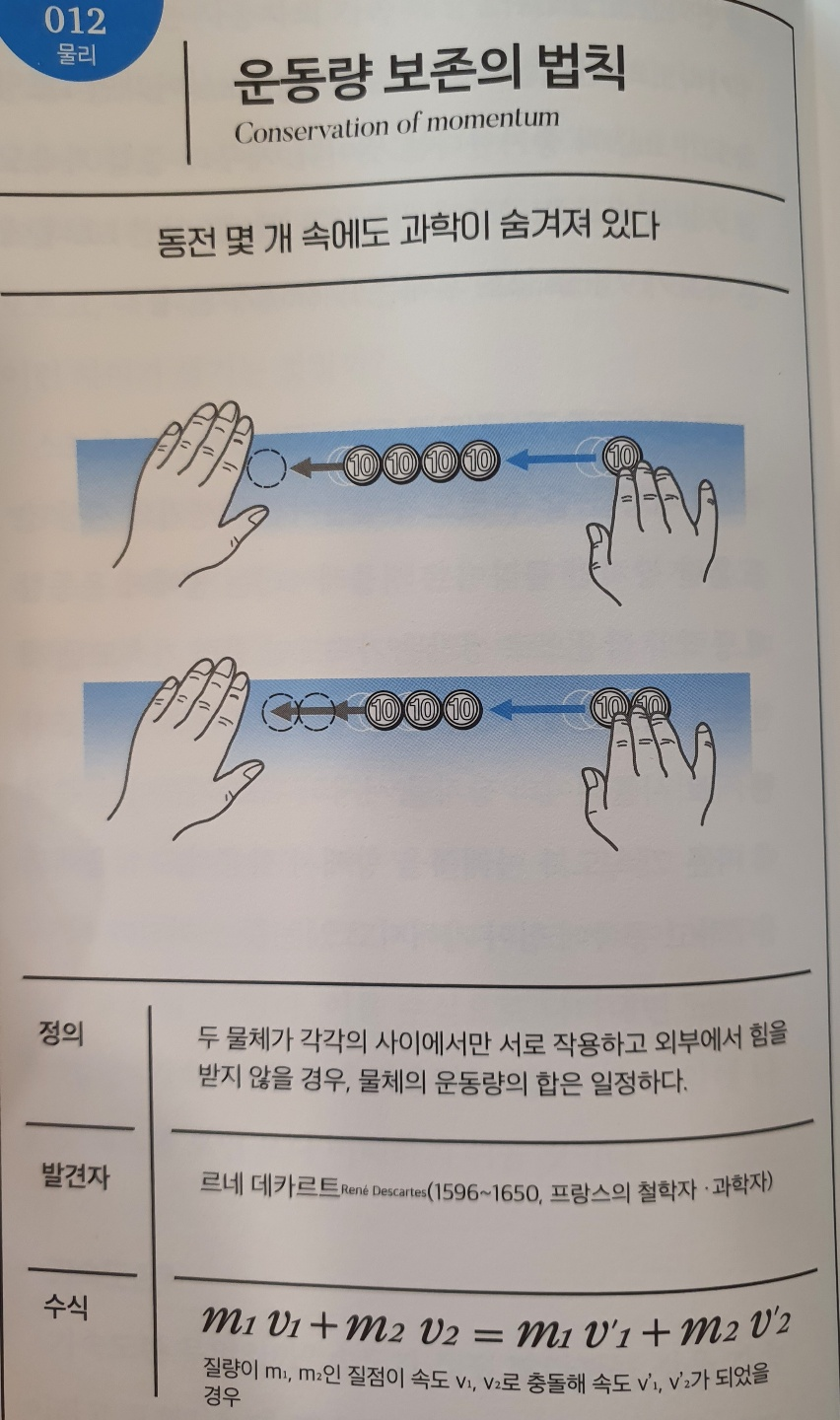
No.012 운동량 보존의 법칙
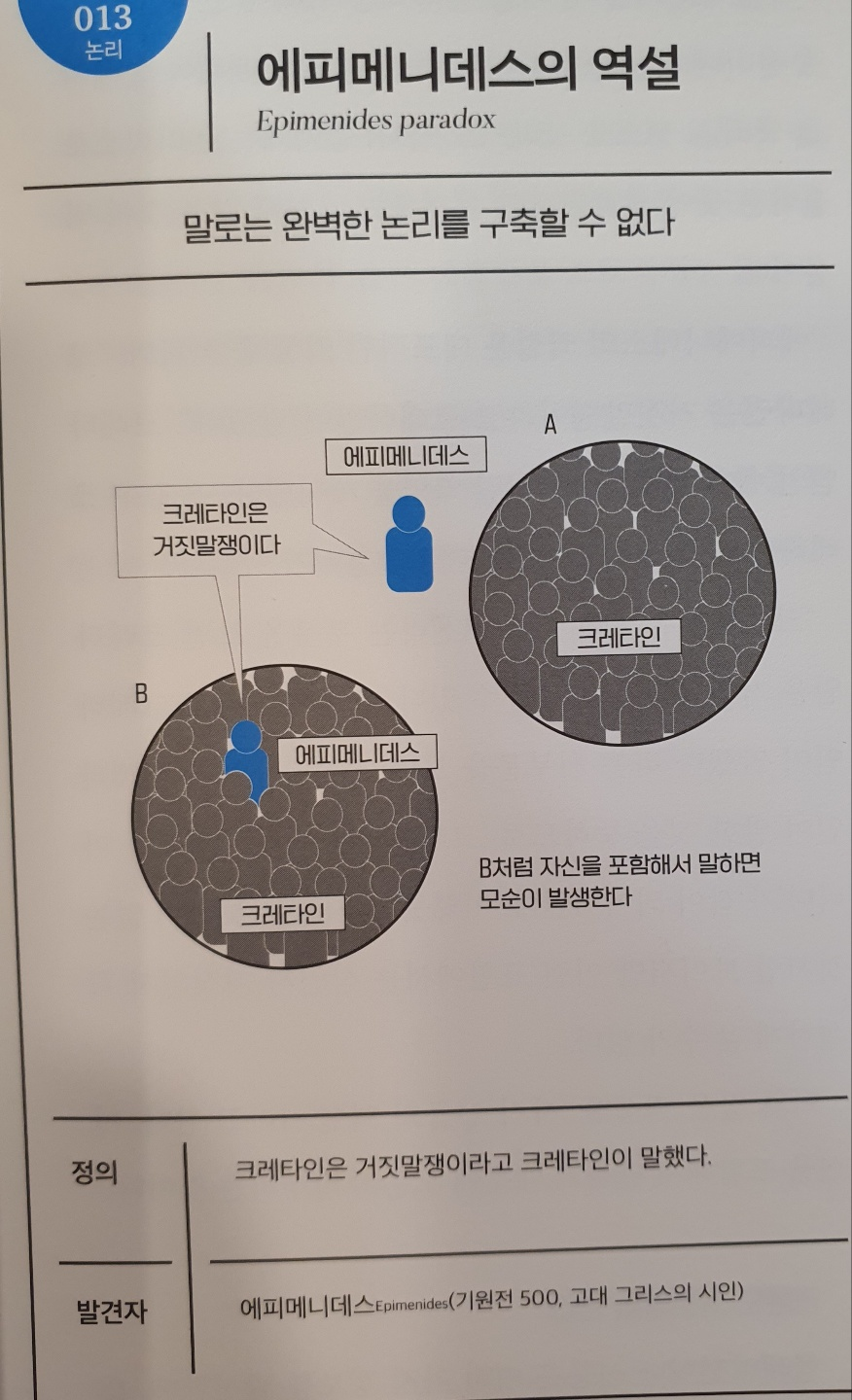
No.013 에피메니데스의 역설
No.014 에라토스테네스의 체
No.015 장거리 연애의 법칙
No.016 엔트로피 증가의 법칙
No.017 엠메르트의 법칙
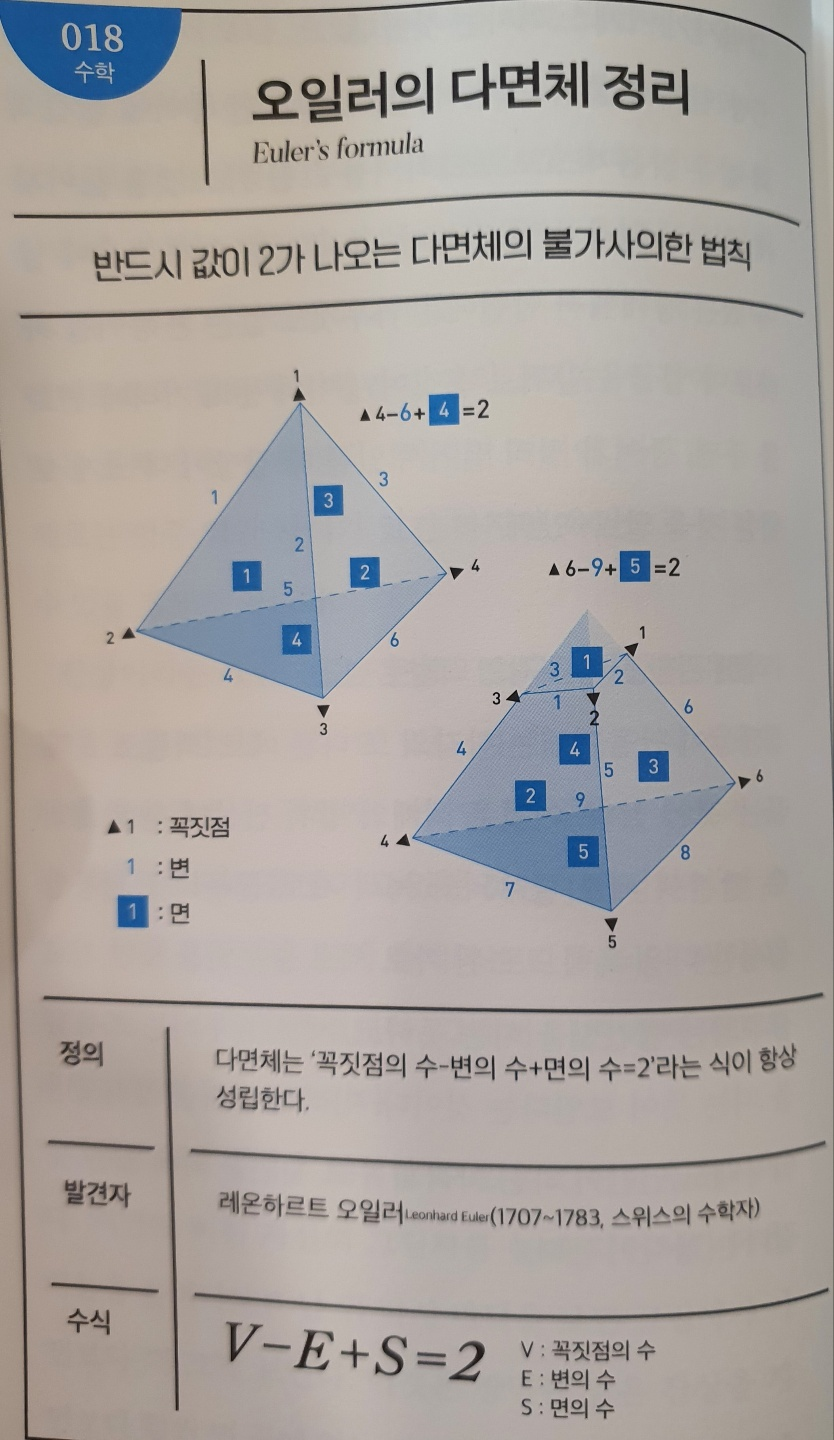
No.018 오일러의 다면체 정리
No.019 황금비
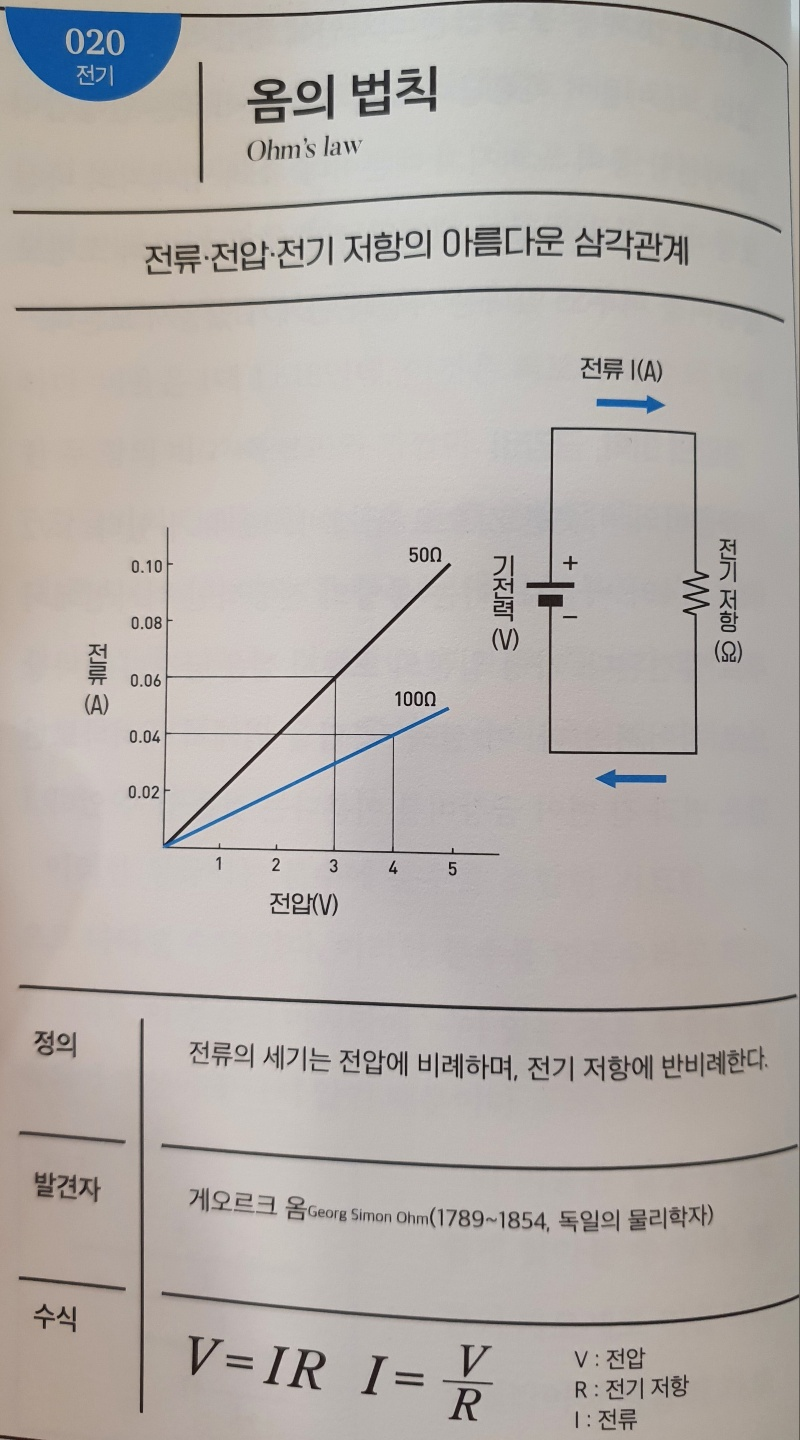
No.020 옴의 법칙
No.021 오컴의 면도날
No.022 올베르스의 역설
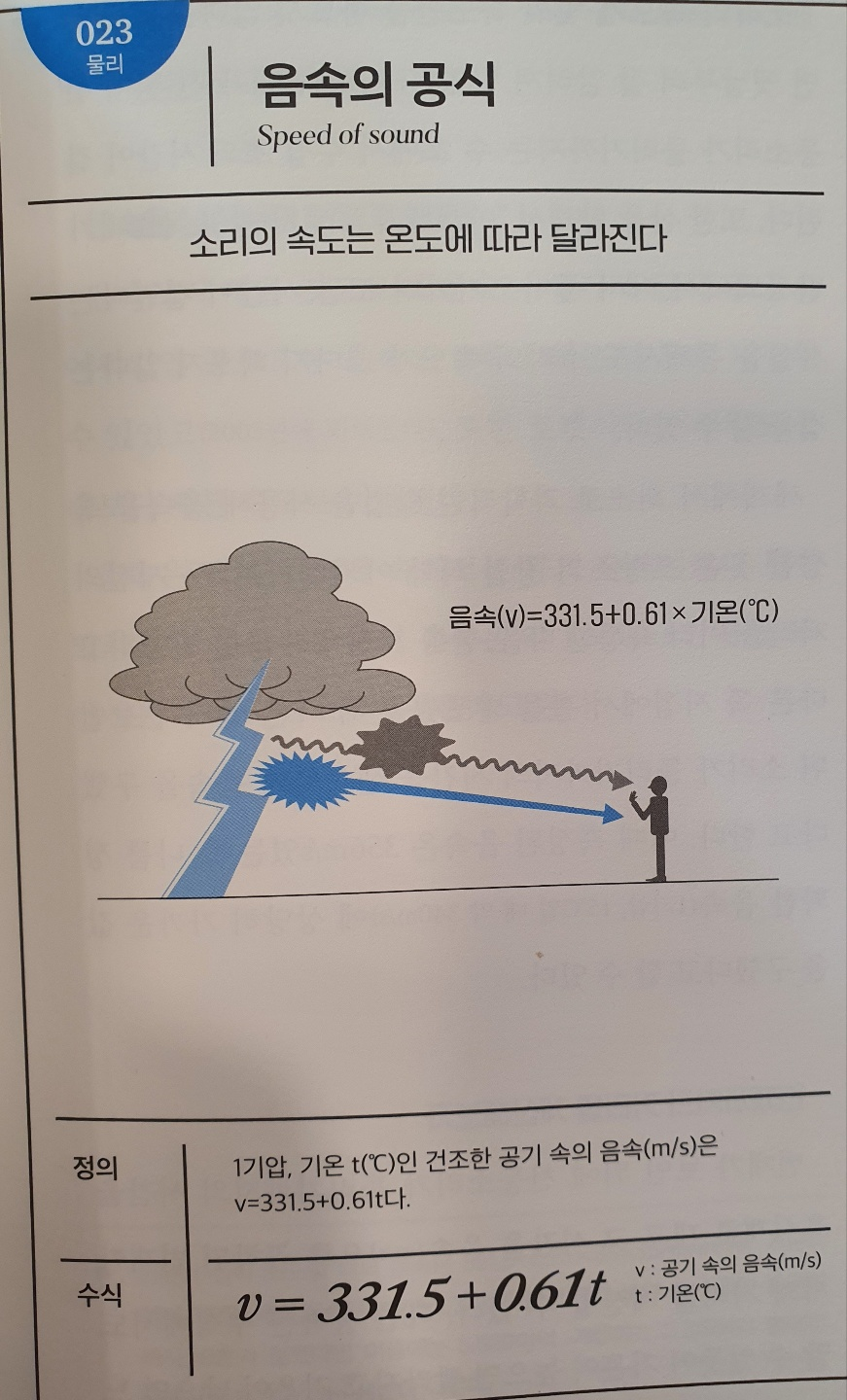
No.023 음속의 공식
No.024 각운동량 보존의 법칙
No.025 칵테일파티 효과
Part. 2
No.026 카발리에리의 정리
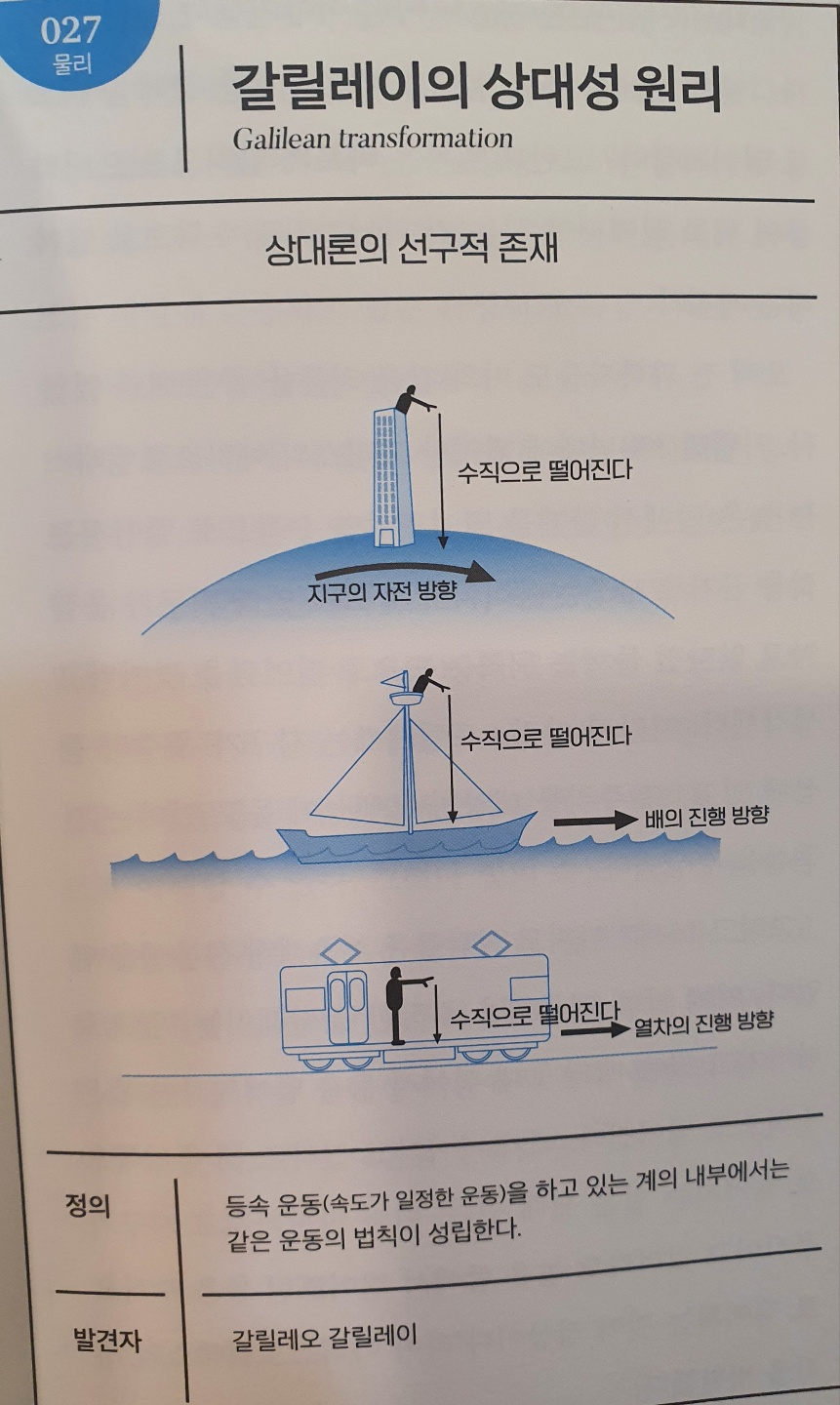
No.027 갈릴레이의 상대성 원리
No.028 관성의 법칙(운동의 제1법칙)
No.029 캐즘 이론
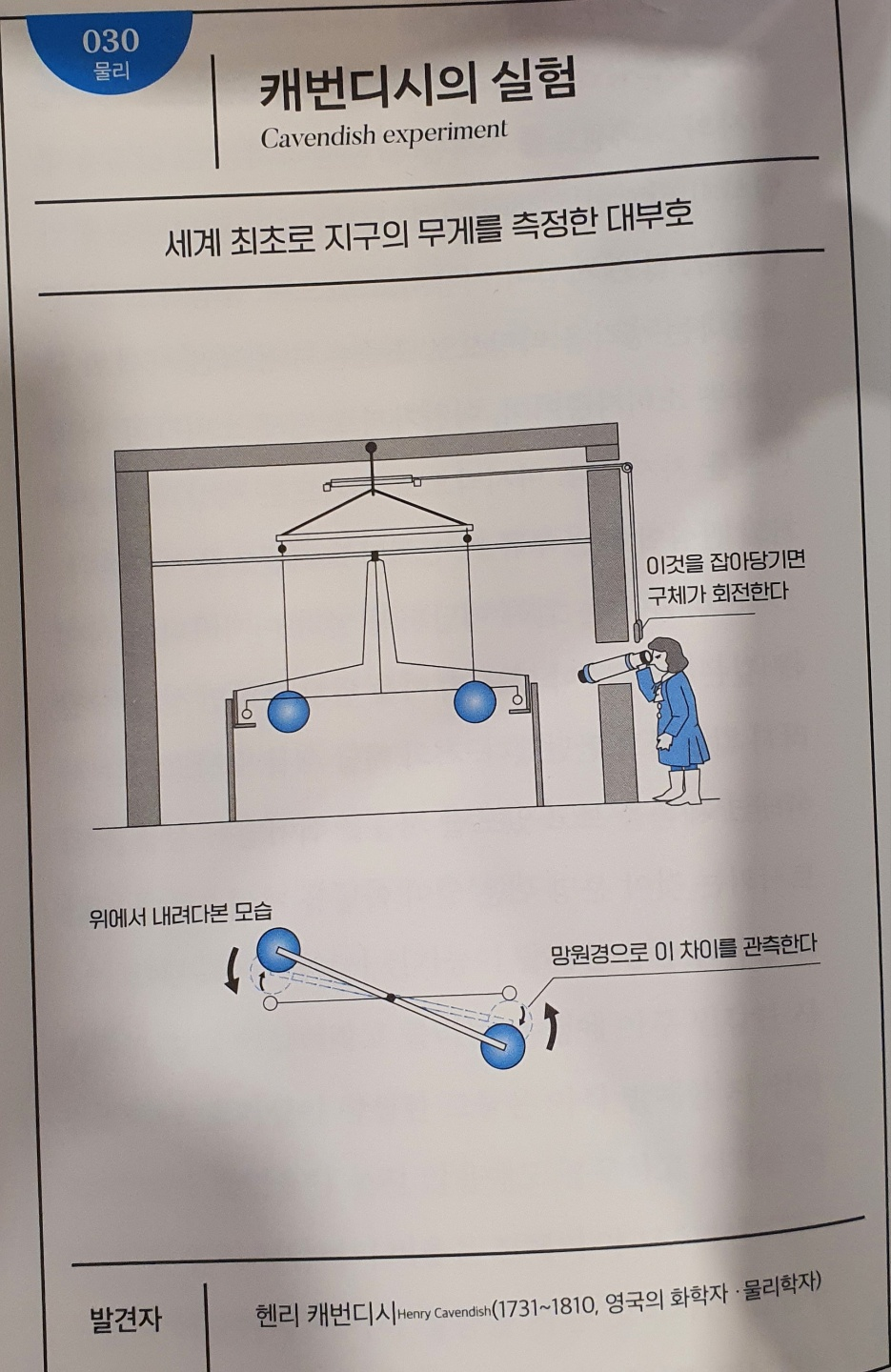
No.030 캐번디시의 실험
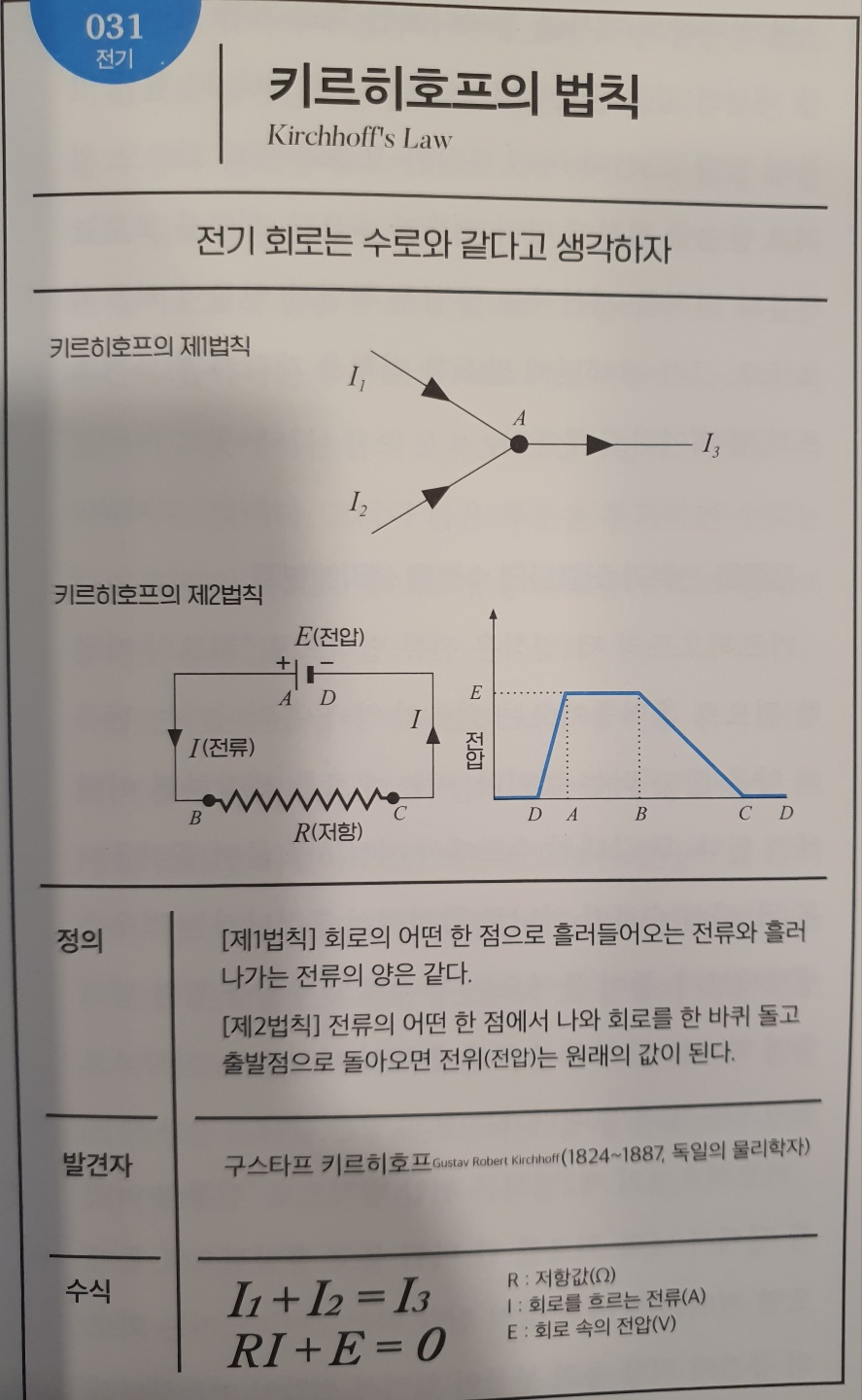
No.031 키르히호프의 법칙
No.032 쿨롱의 법칙
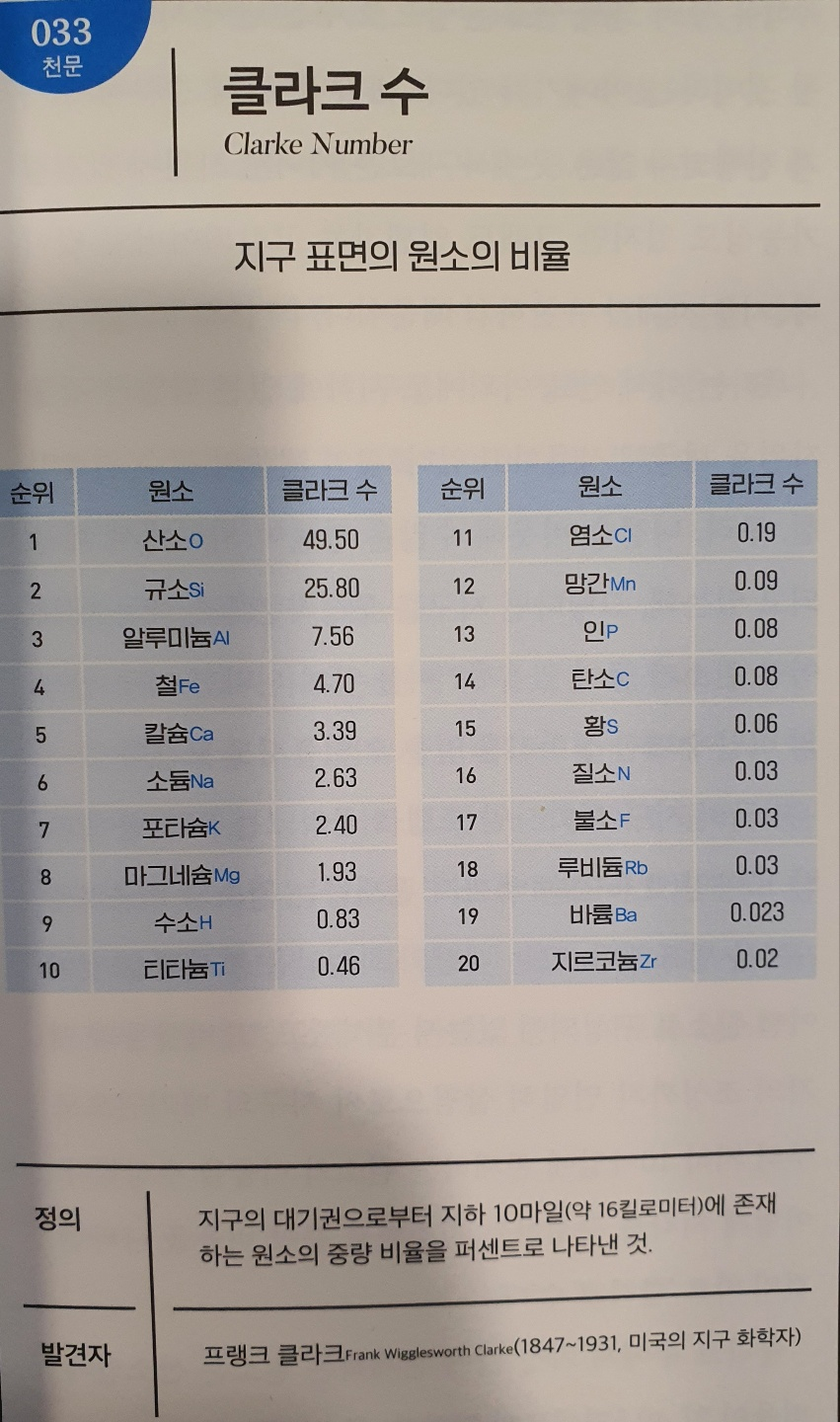
No.033 클라크 수
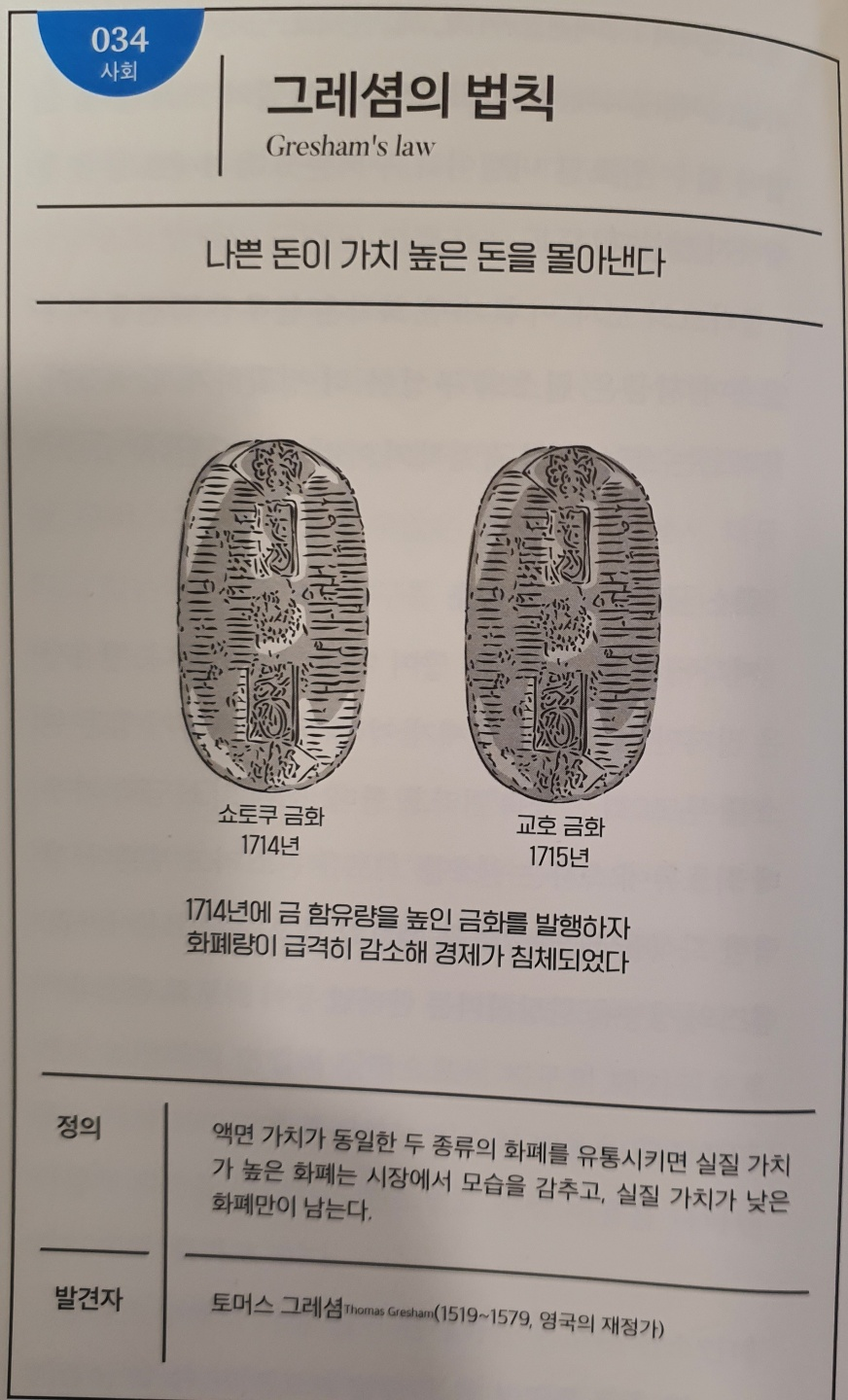
No.034 그레셤의 법칙
No.035 그로슈의 법칙
No.036 게슈탈트 심리학
No.037 케플러의 법칙
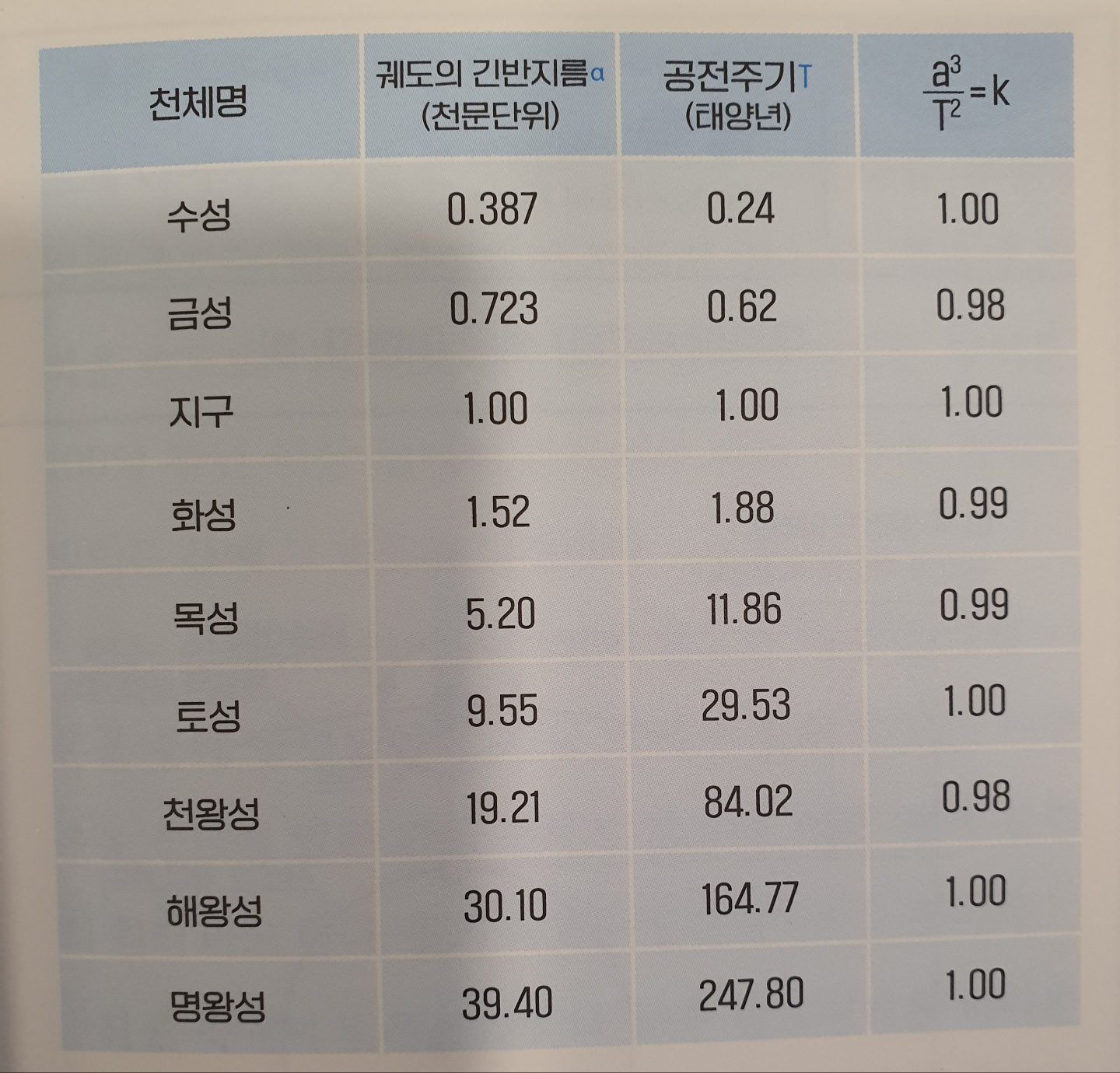
No.038 광속
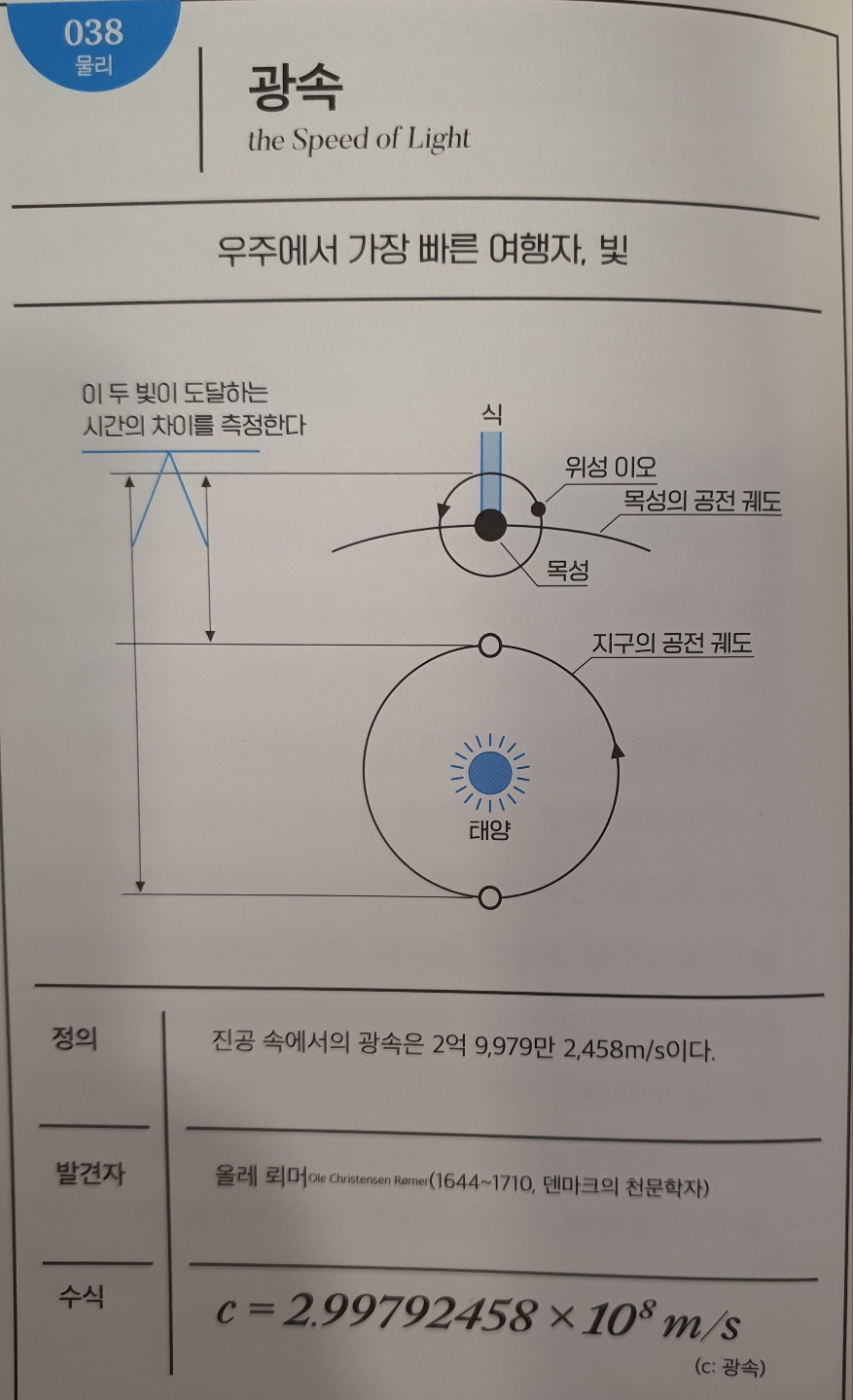
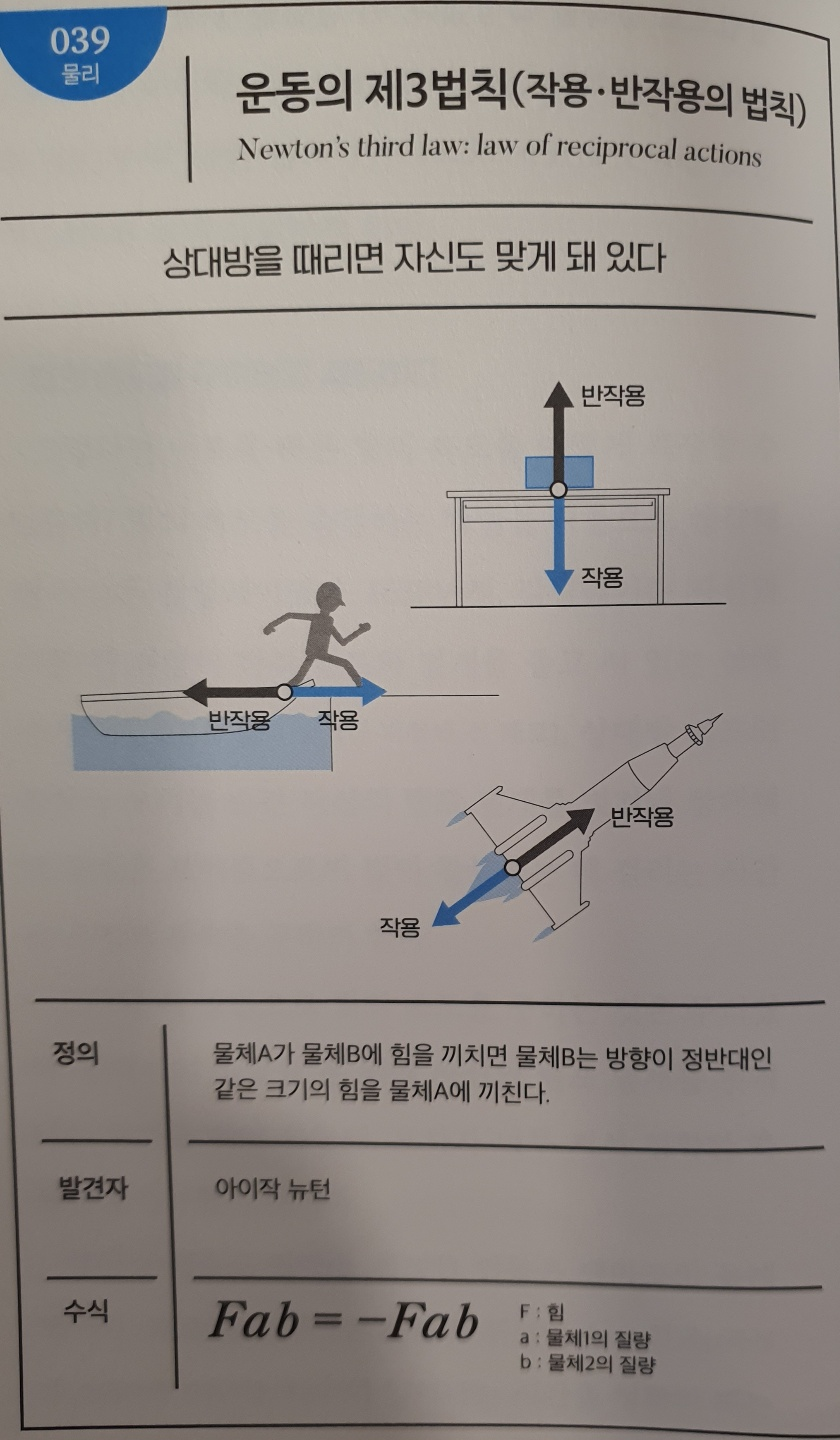
No.039 운동의 제3법칙(작용ㆍ반작용의 법칙)
No.040 질량 보존의 법칙
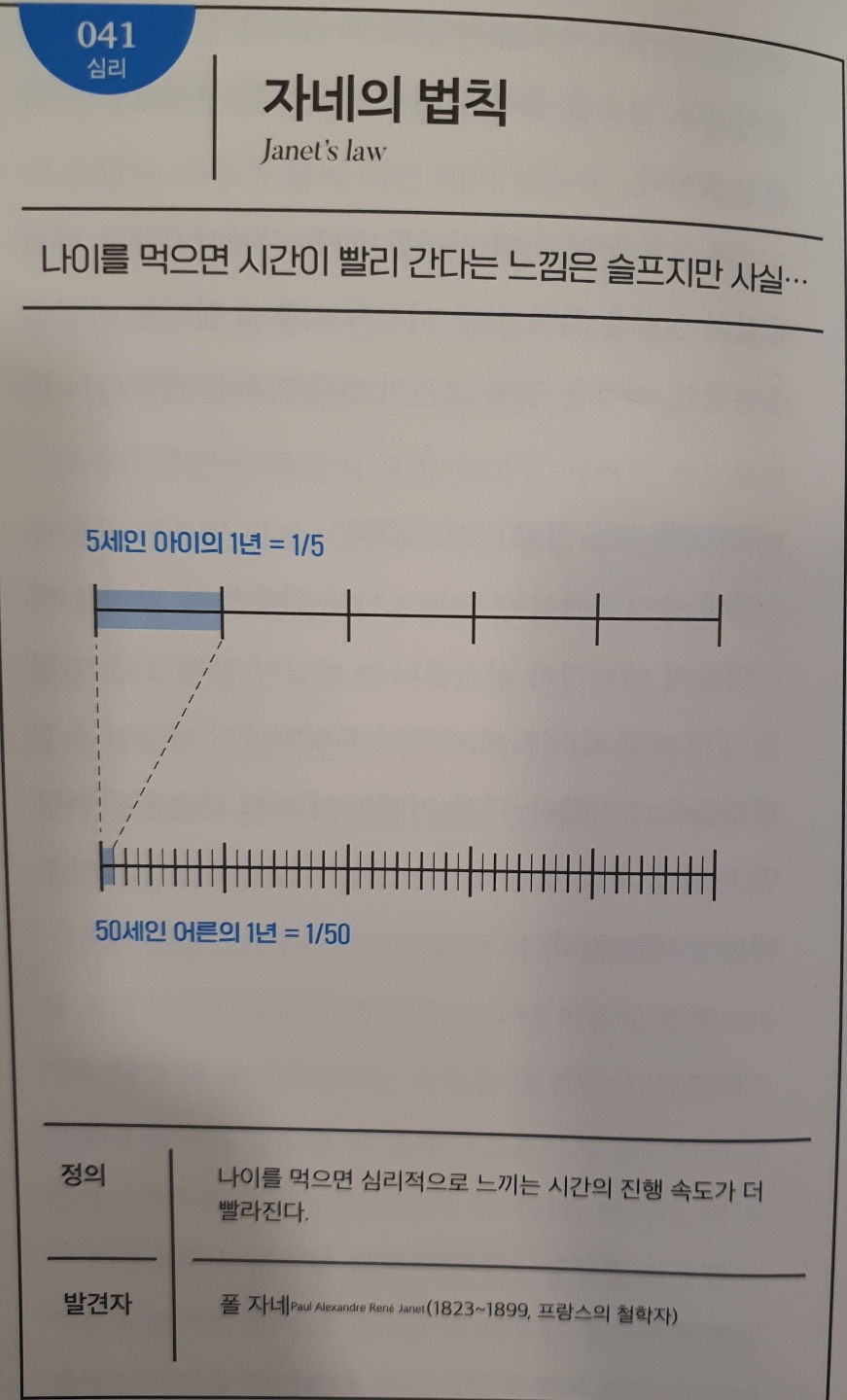
No.041 자네의 법칙
No.042 섀넌의 정리
No.043 샤를의 법칙
No.044 주기율표
No.045 죄수의 딜레마
No.046 중력 가속도
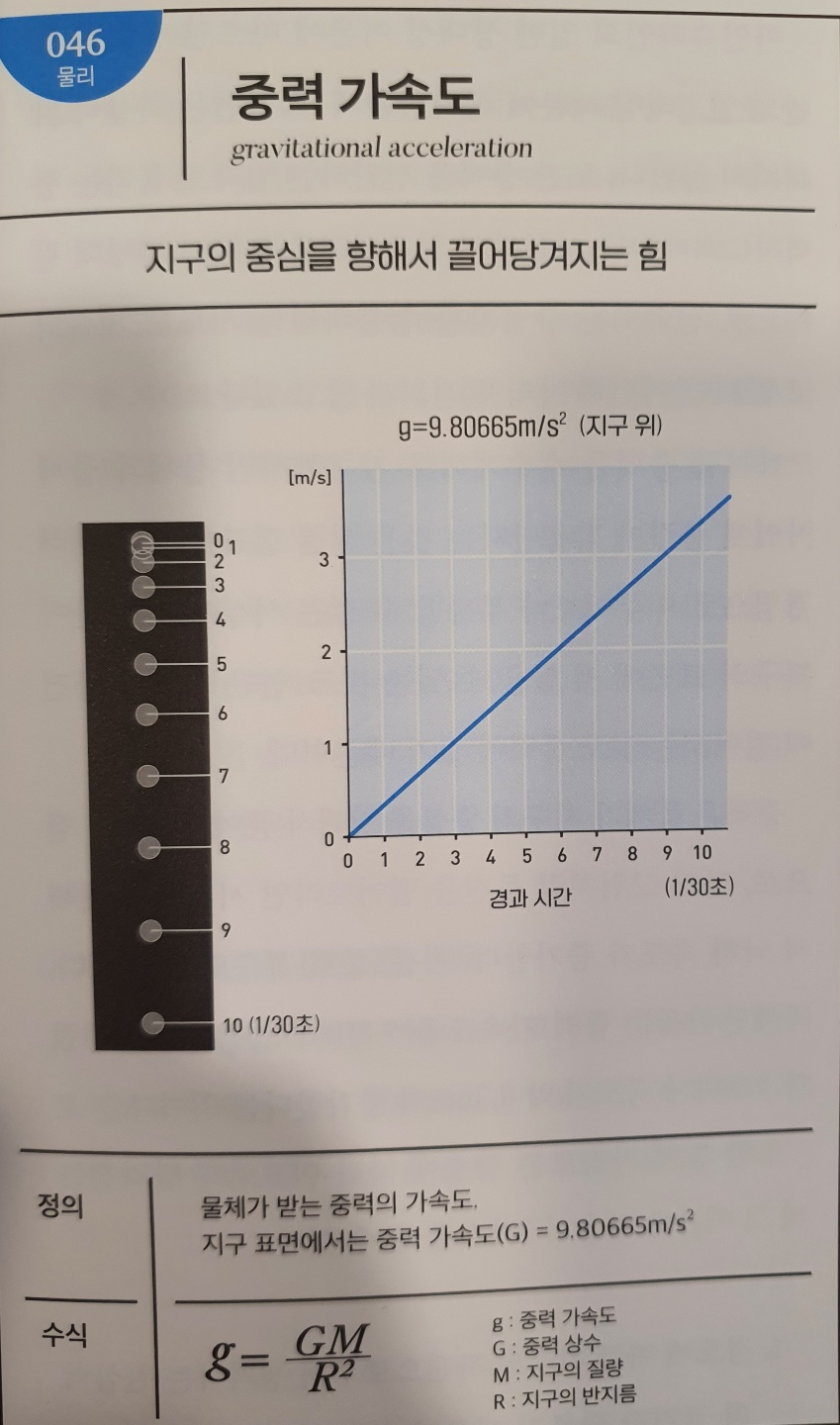
No.047 줄의 법칙
No.048 슈푀러의 법칙
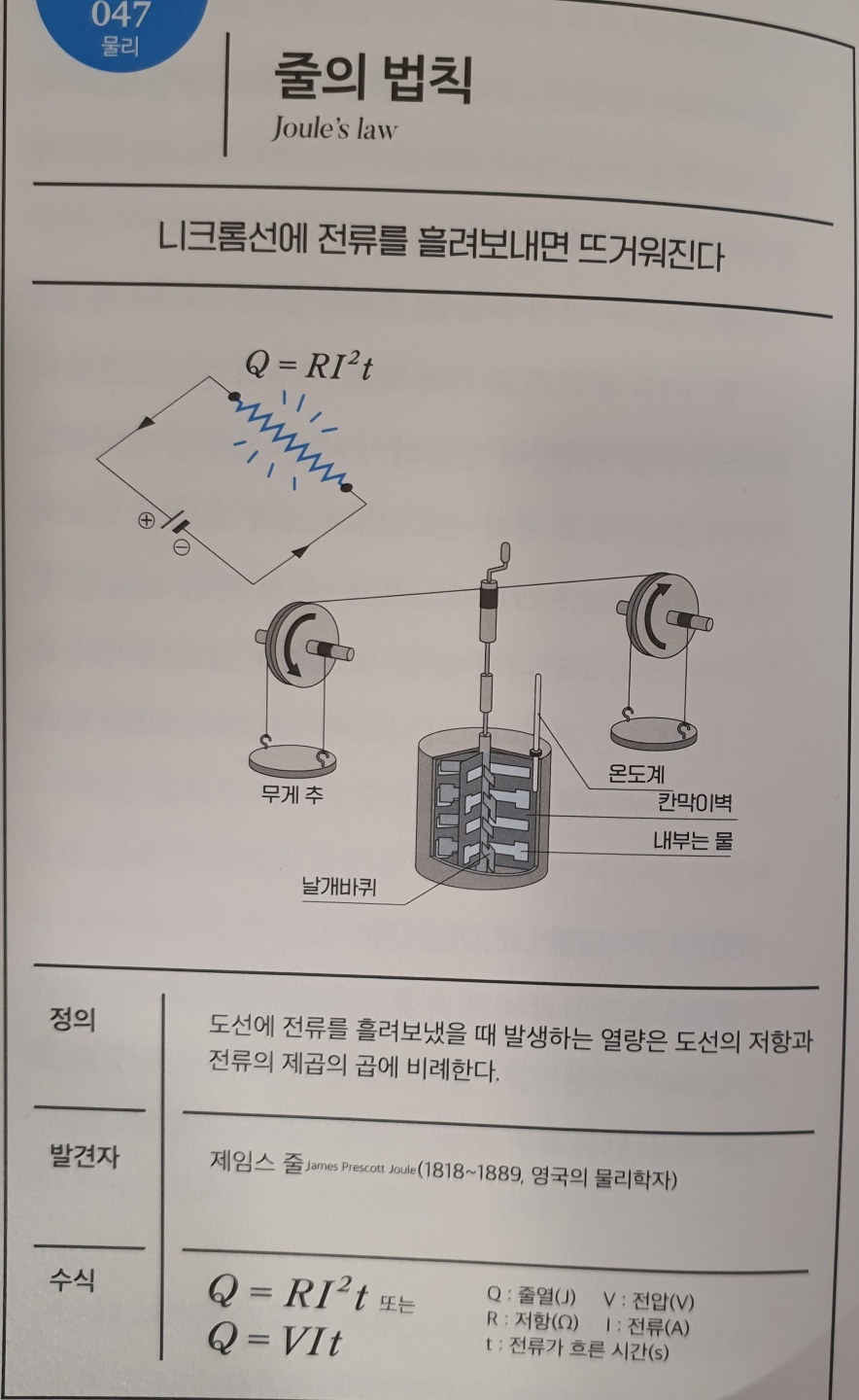
No.049 스넬의 법칙
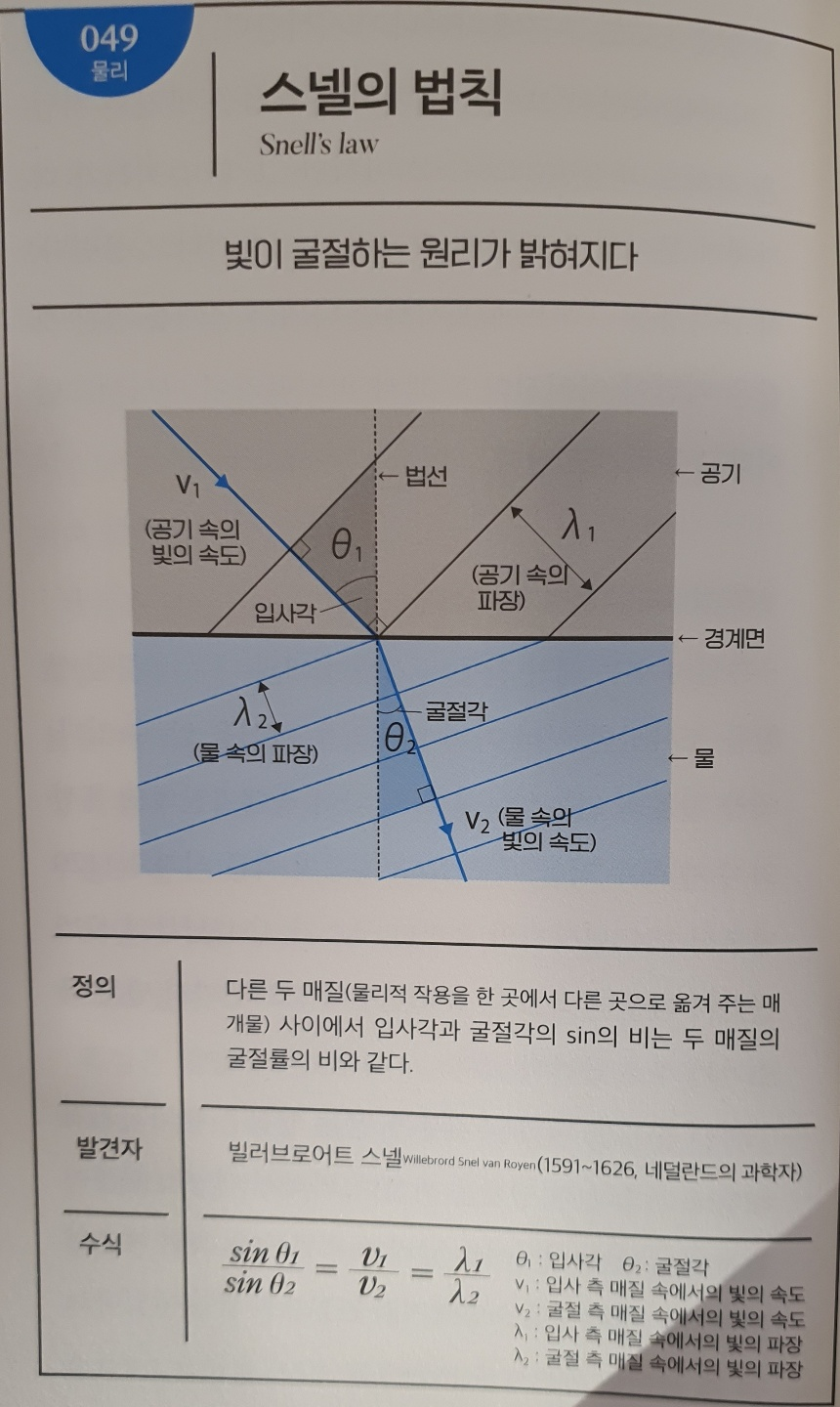
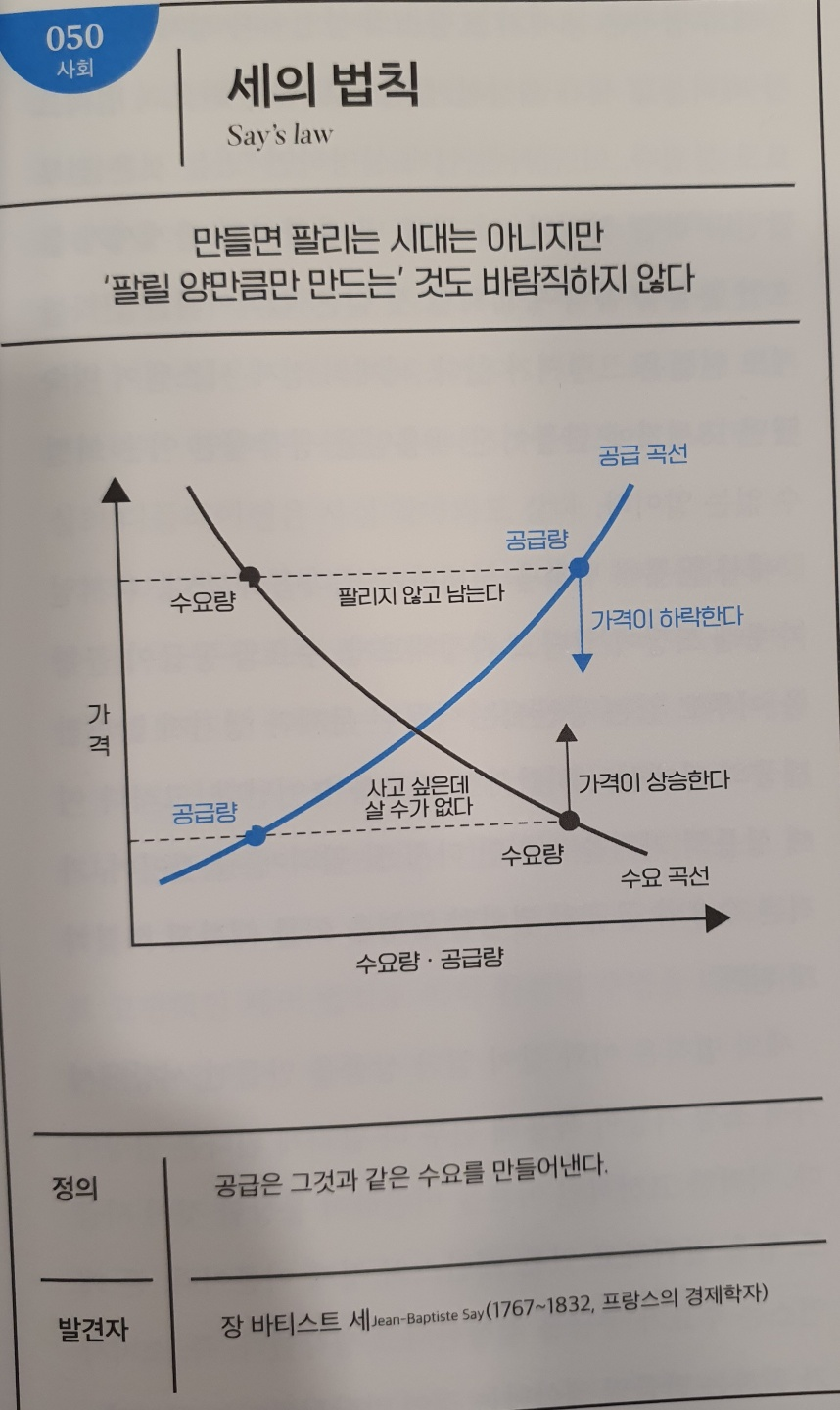
No.050 세의 법칙
No.051 제논의 역설
No.052 실무율
No.053 큰 수의 법칙
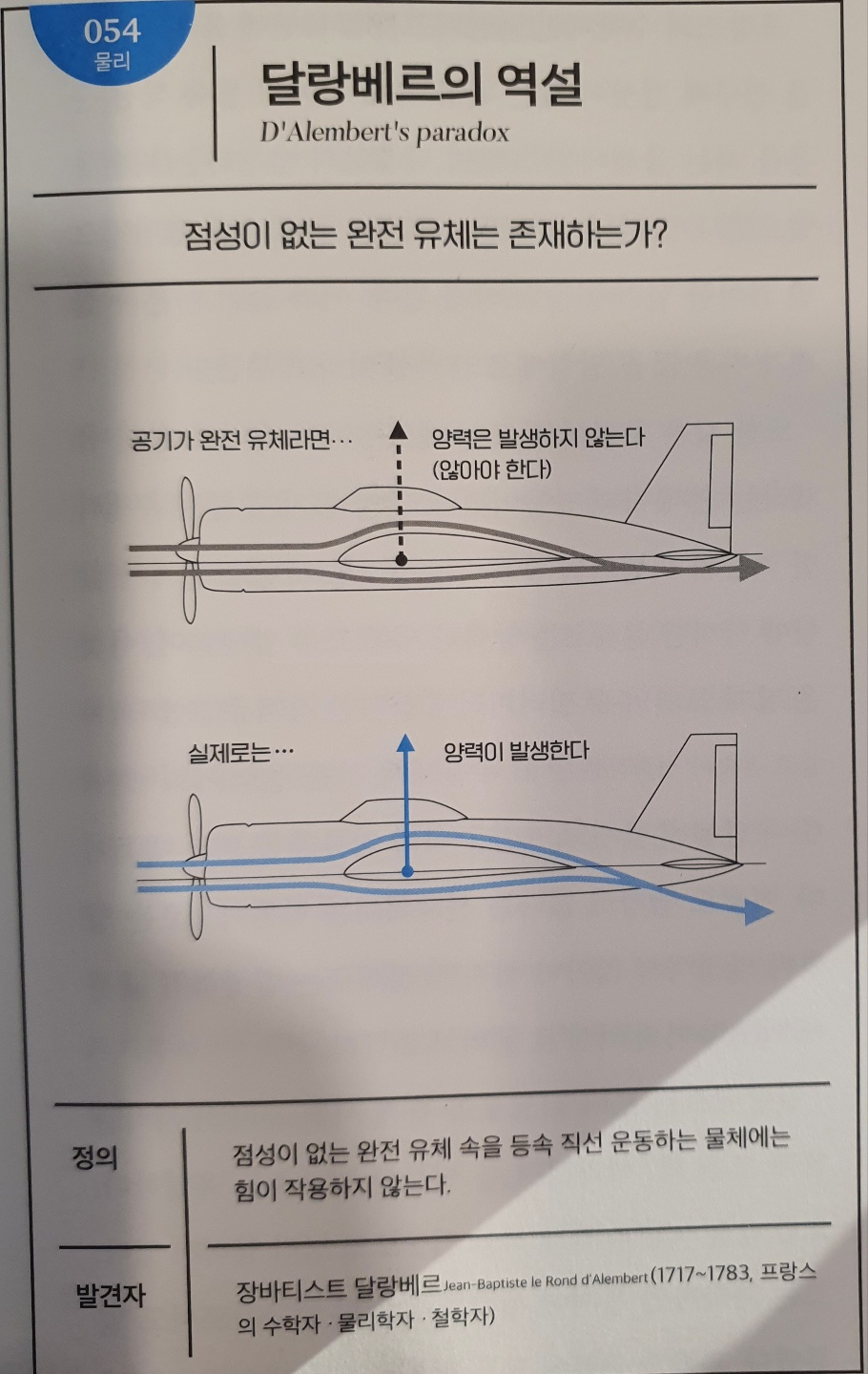
No.054 달랑베르의 역설
Part. 3
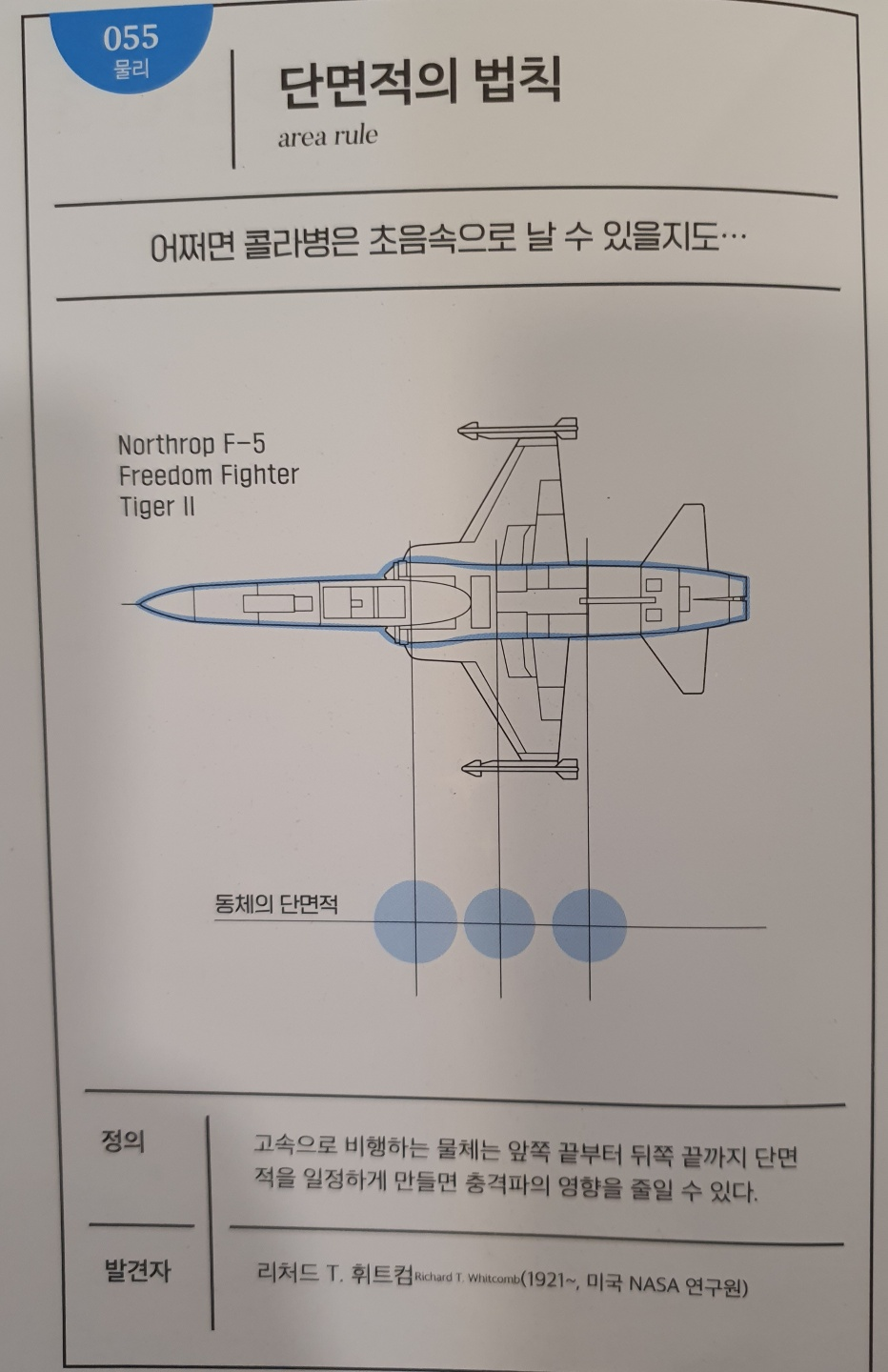
No.055 단면적의 법칙
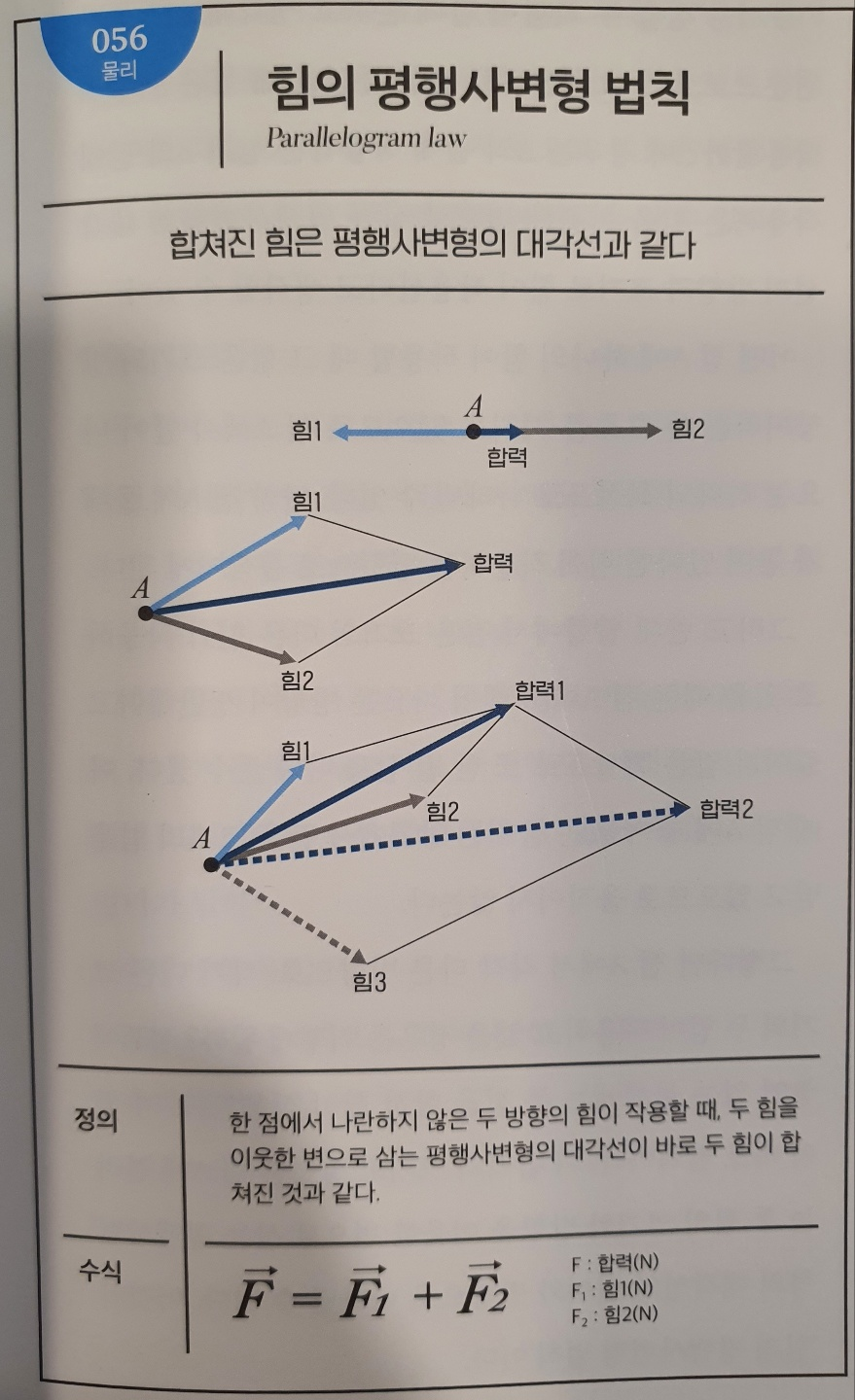
No.056 힘의 평행사변형 법칙
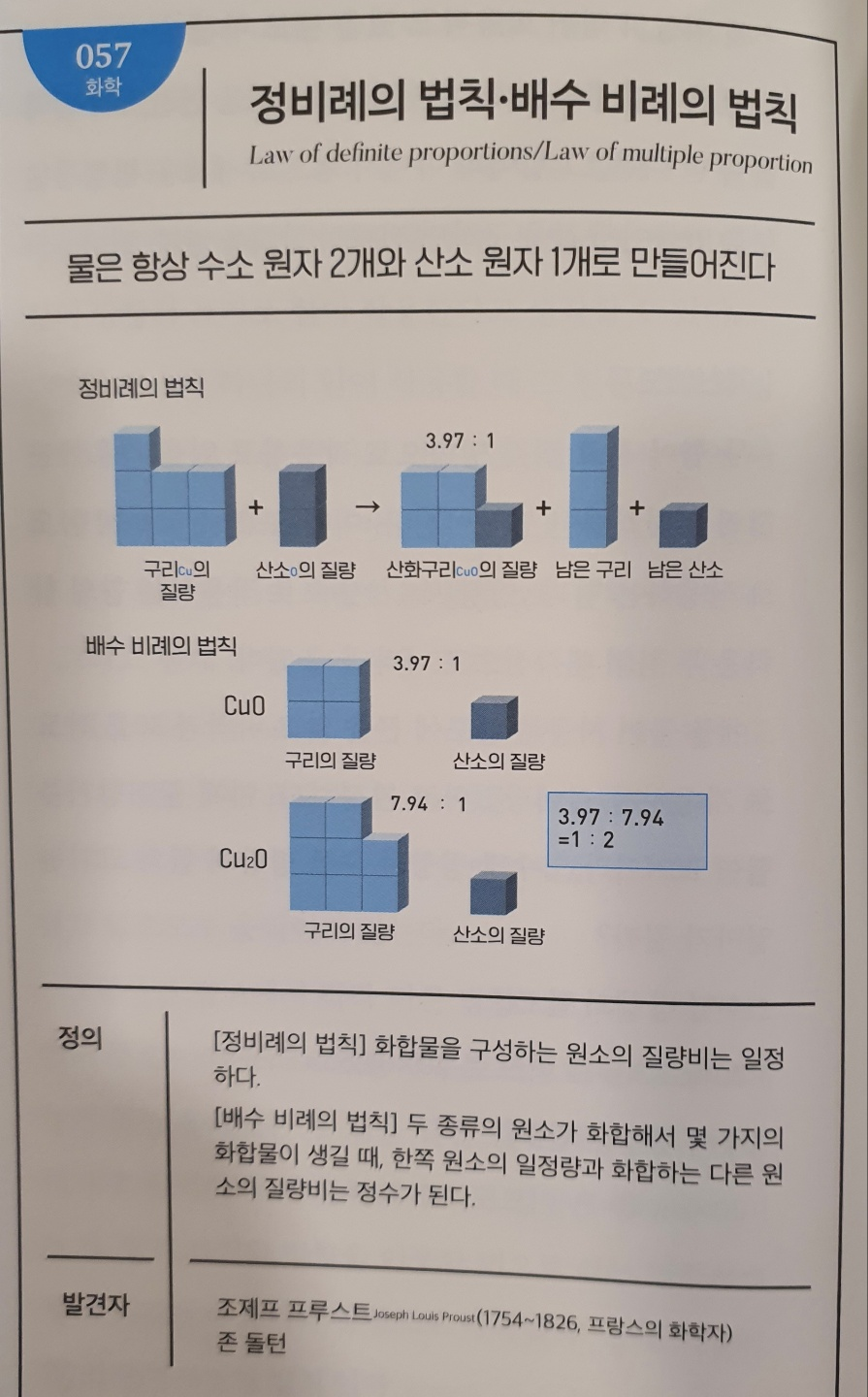
No.057 정비례의 법칙·배수 비례의 법칙
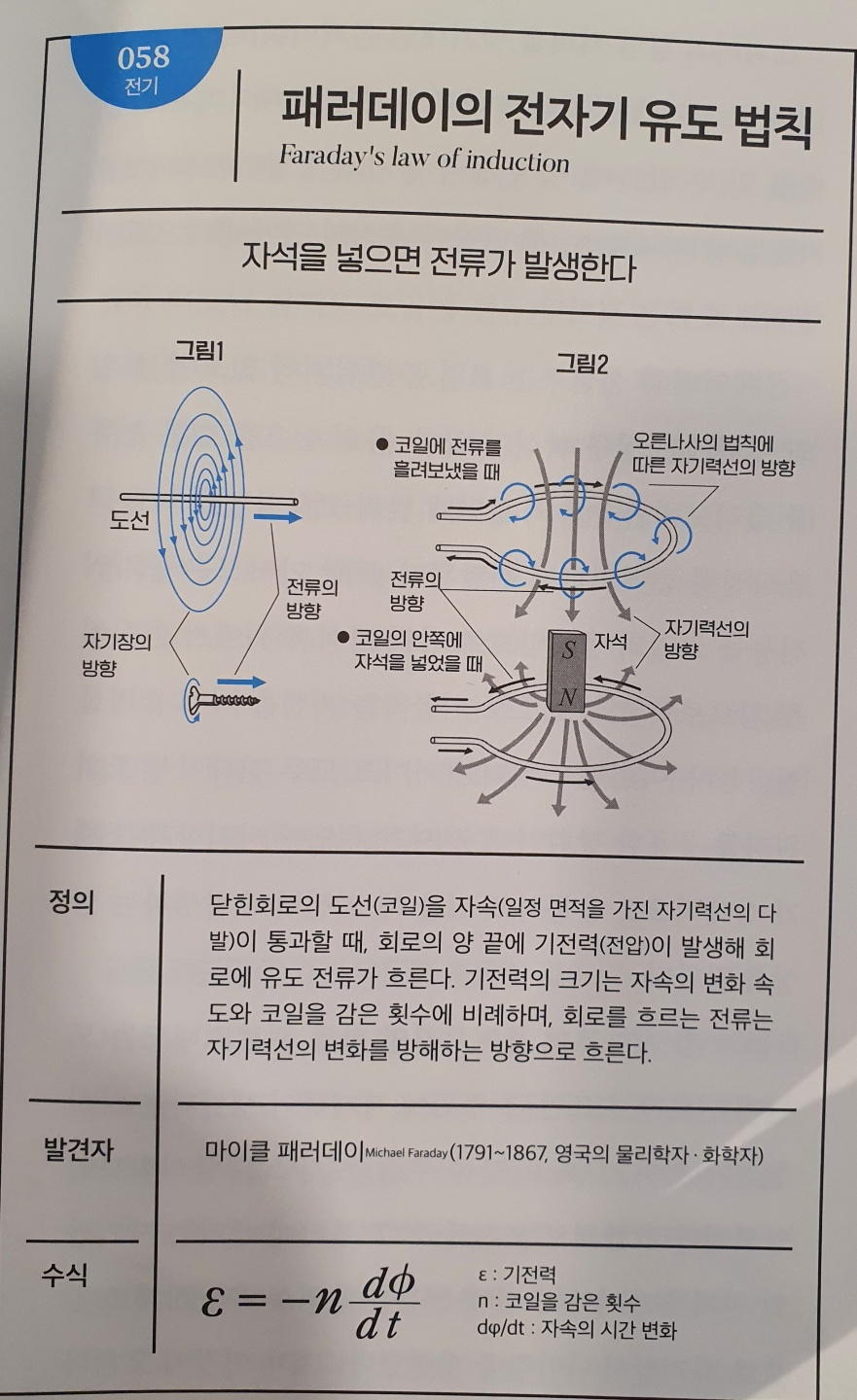
No.058 패러데이의 전자기 유도 법칙
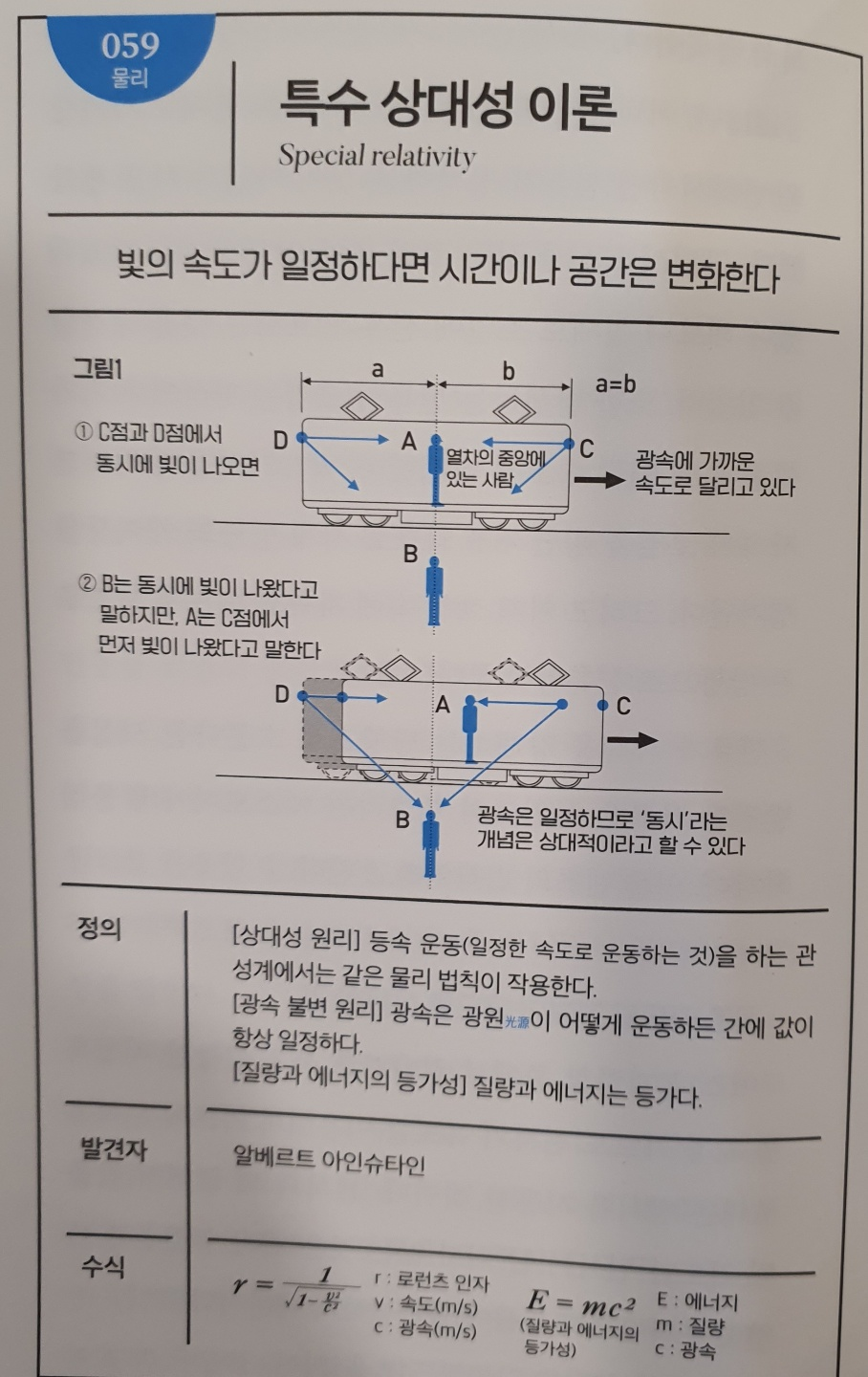
No.059 특수 상대성 이론
No.060 도플러 효과
No.061 드모르간의 법칙
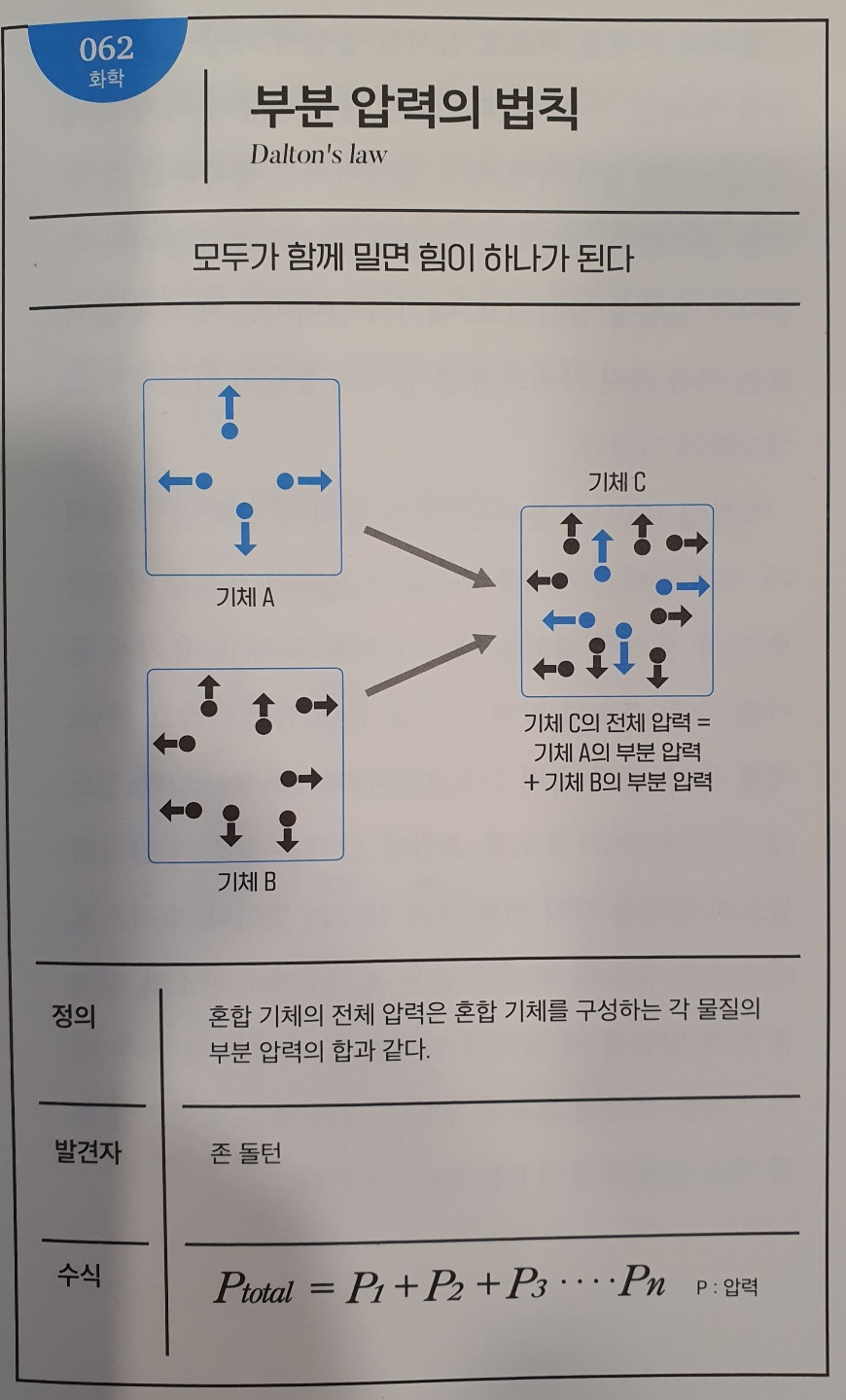
No.062 부분 압력의 법칙
No.063 드레이크 방정식
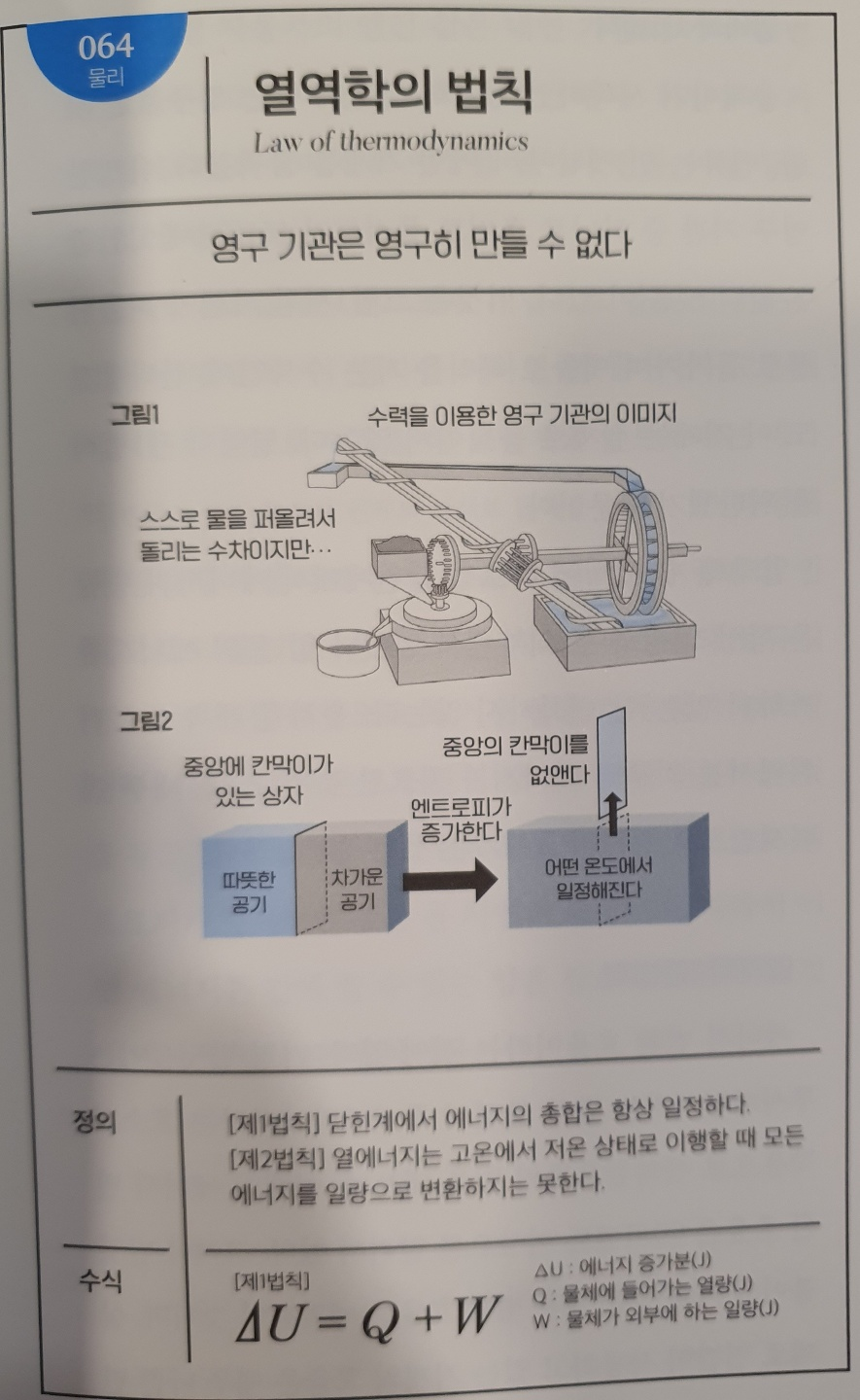
No.064 열역학의 법칙
No.065 파킨슨의 법칙
No.066 하인리히의 법칙
No.067 파스칼의 원리
No.068 나비 효과
No.069 허블의 법칙
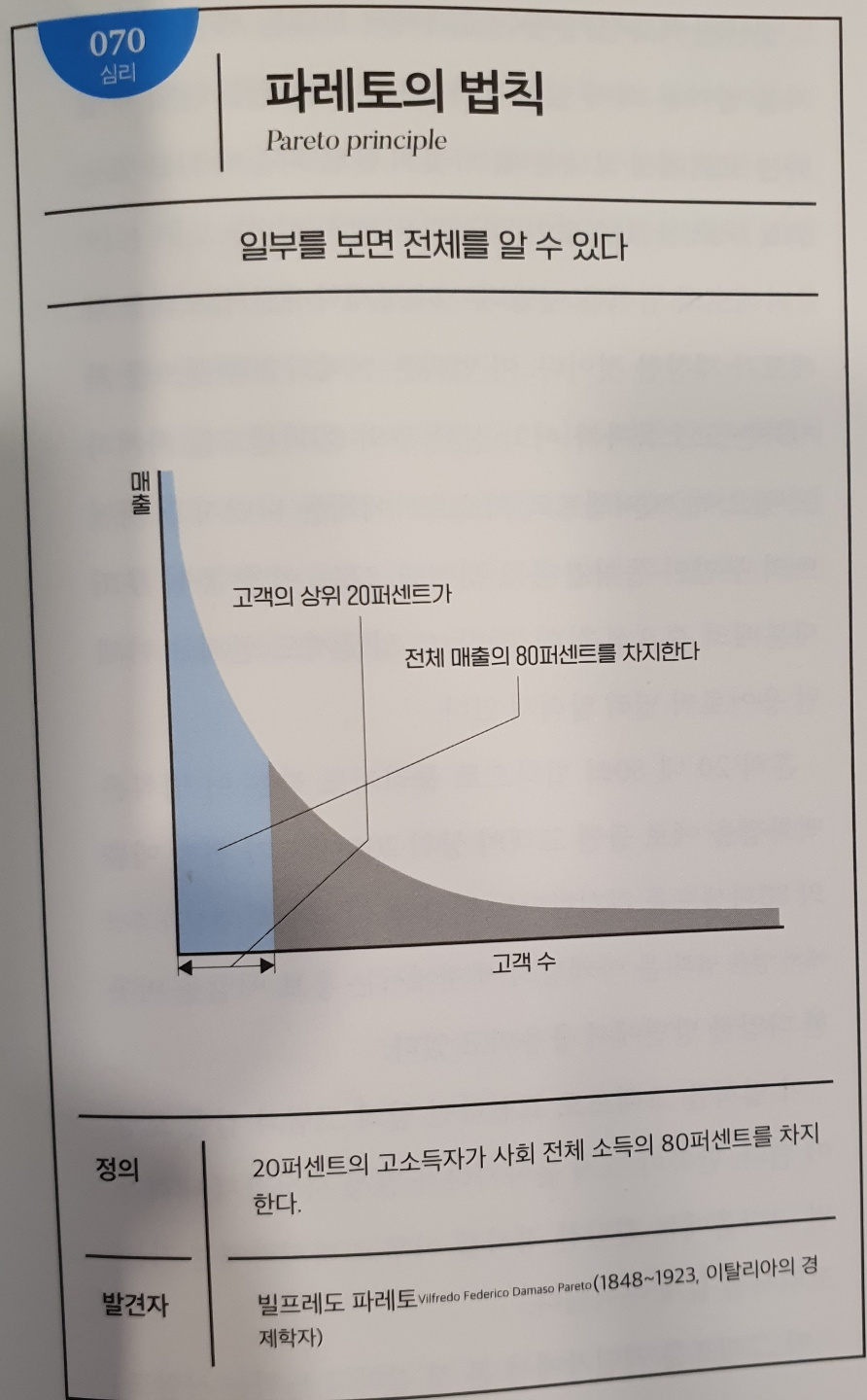
No.070 파레토의 법칙
No.071 반사의 법칙
No.072 만유인력의 법칙
No.073 피터의 법칙
No.074 피타고라스의 정리
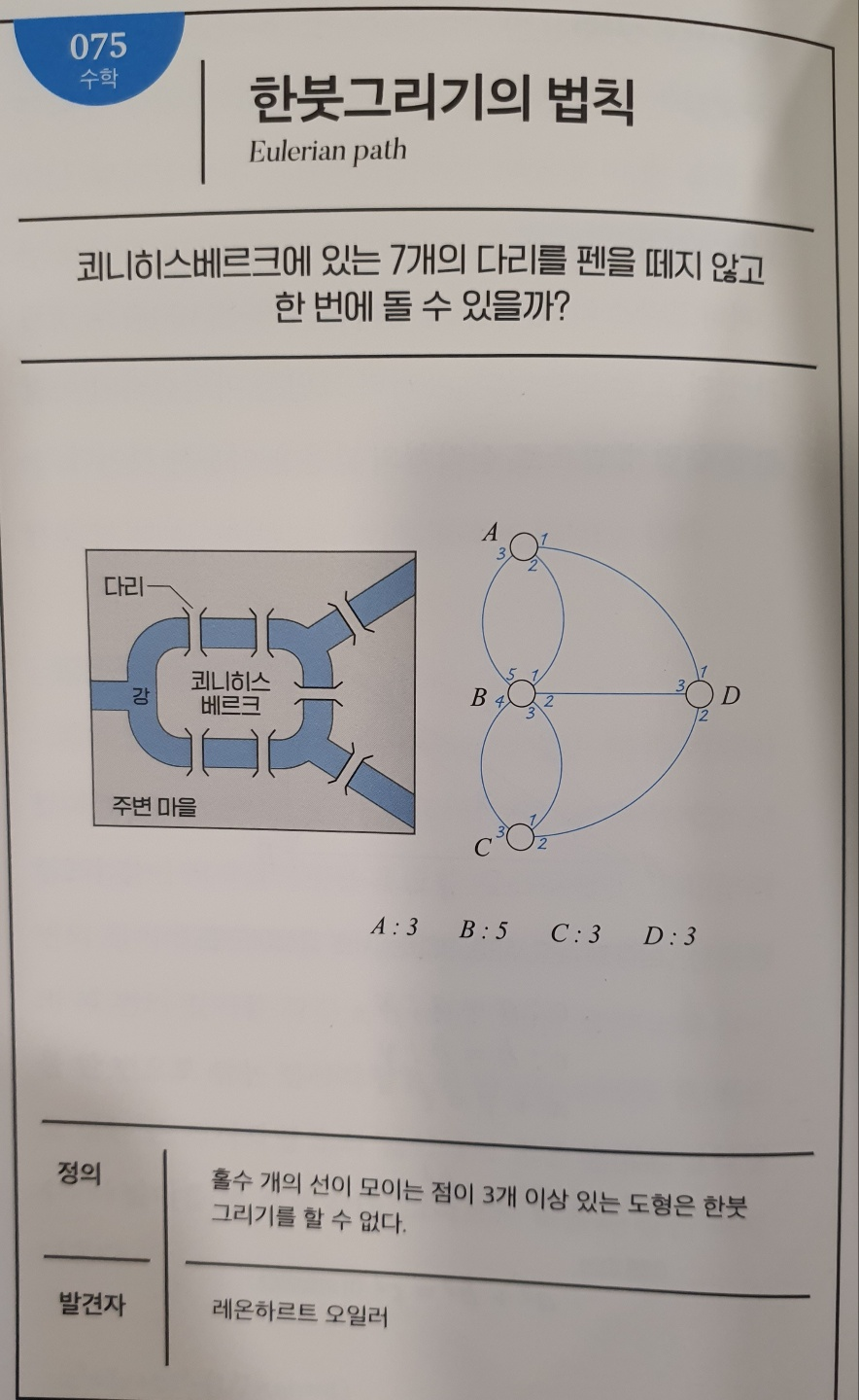
No.075 한붓그리기의 법칙
No.076 패러데이의 전기 분해 법칙
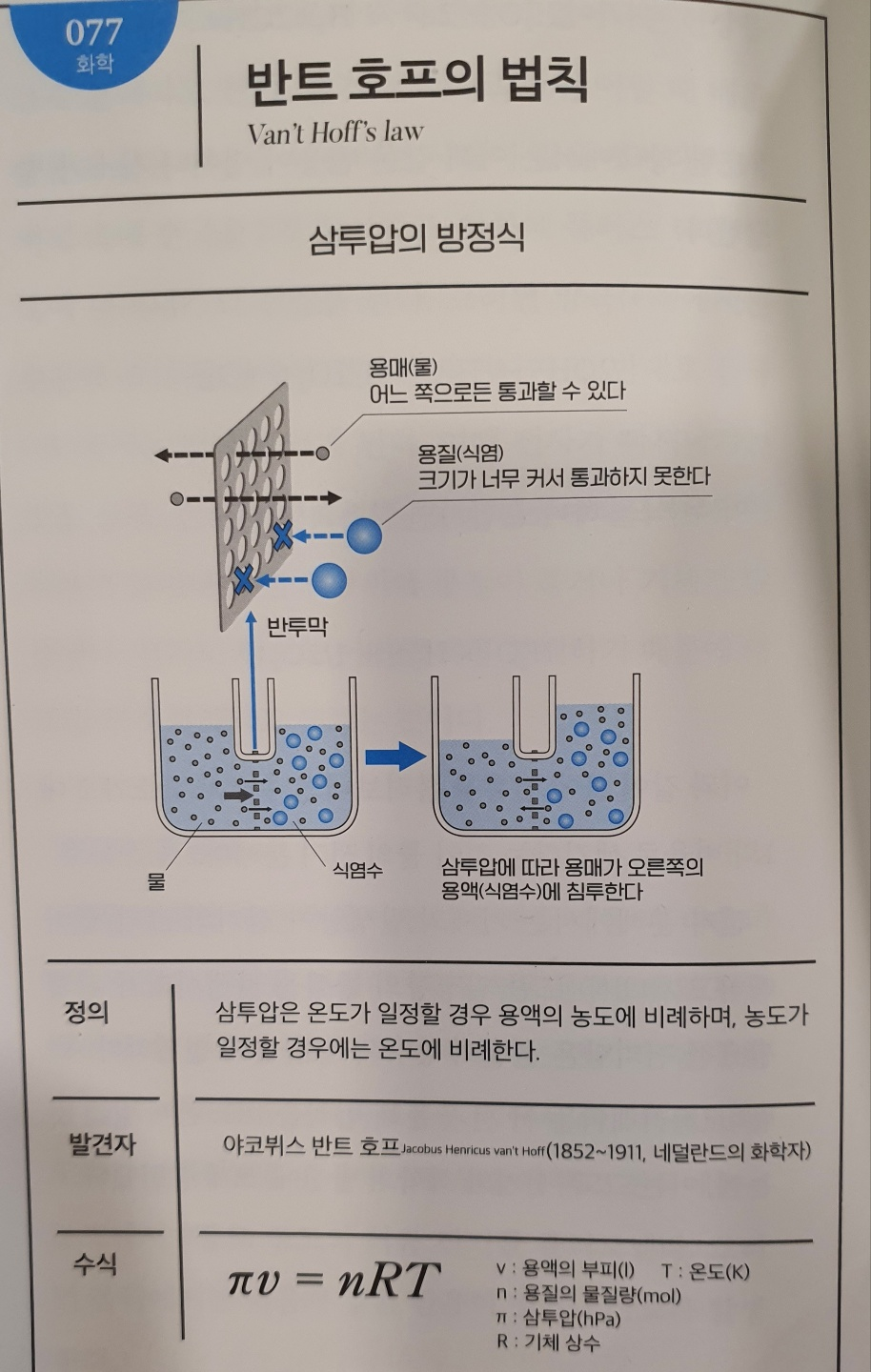
No.077 반트 호프의 법칙
No.078 피츠의 법칙
No.079 피보나치 수
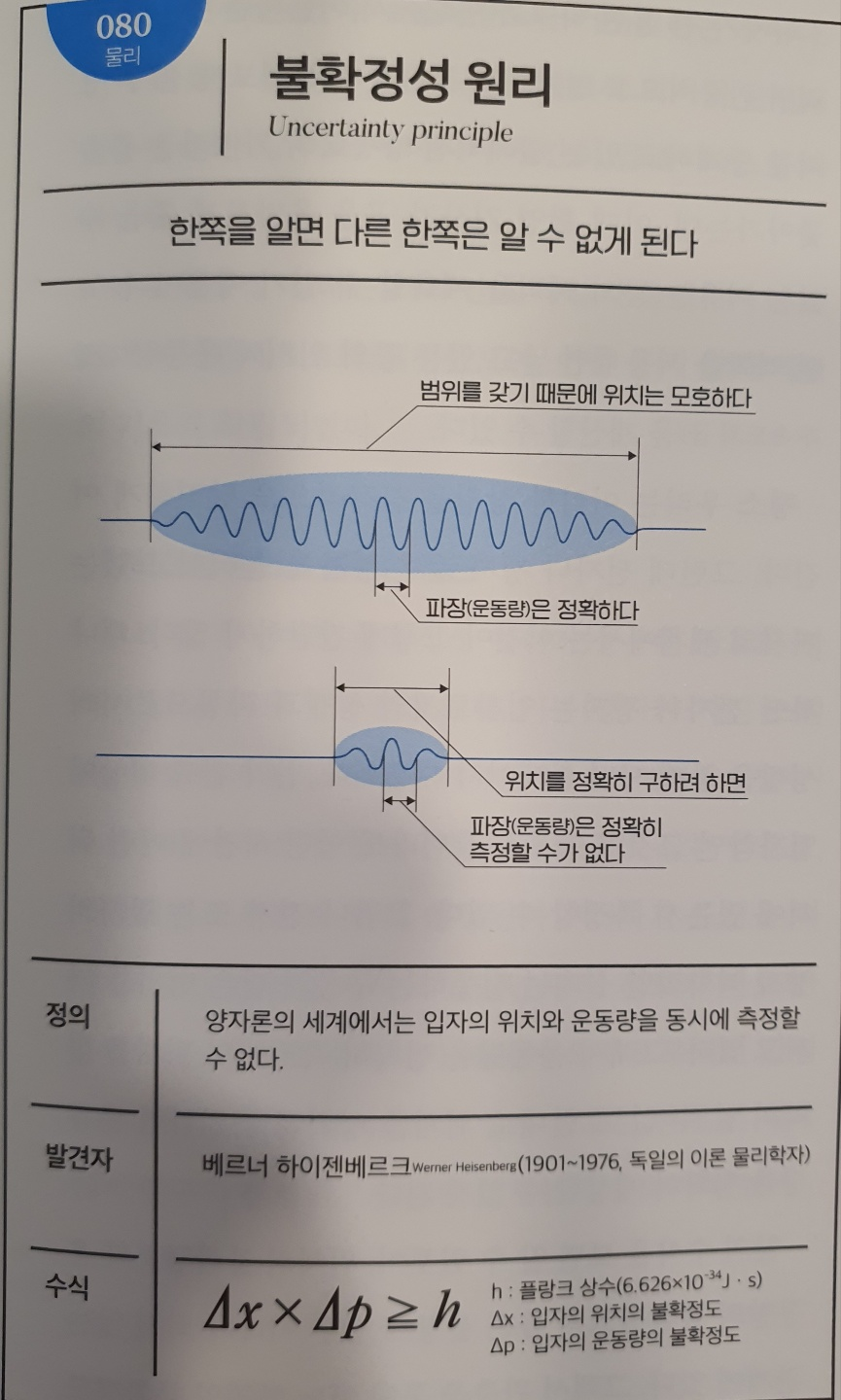
No.080 불확정성 원리
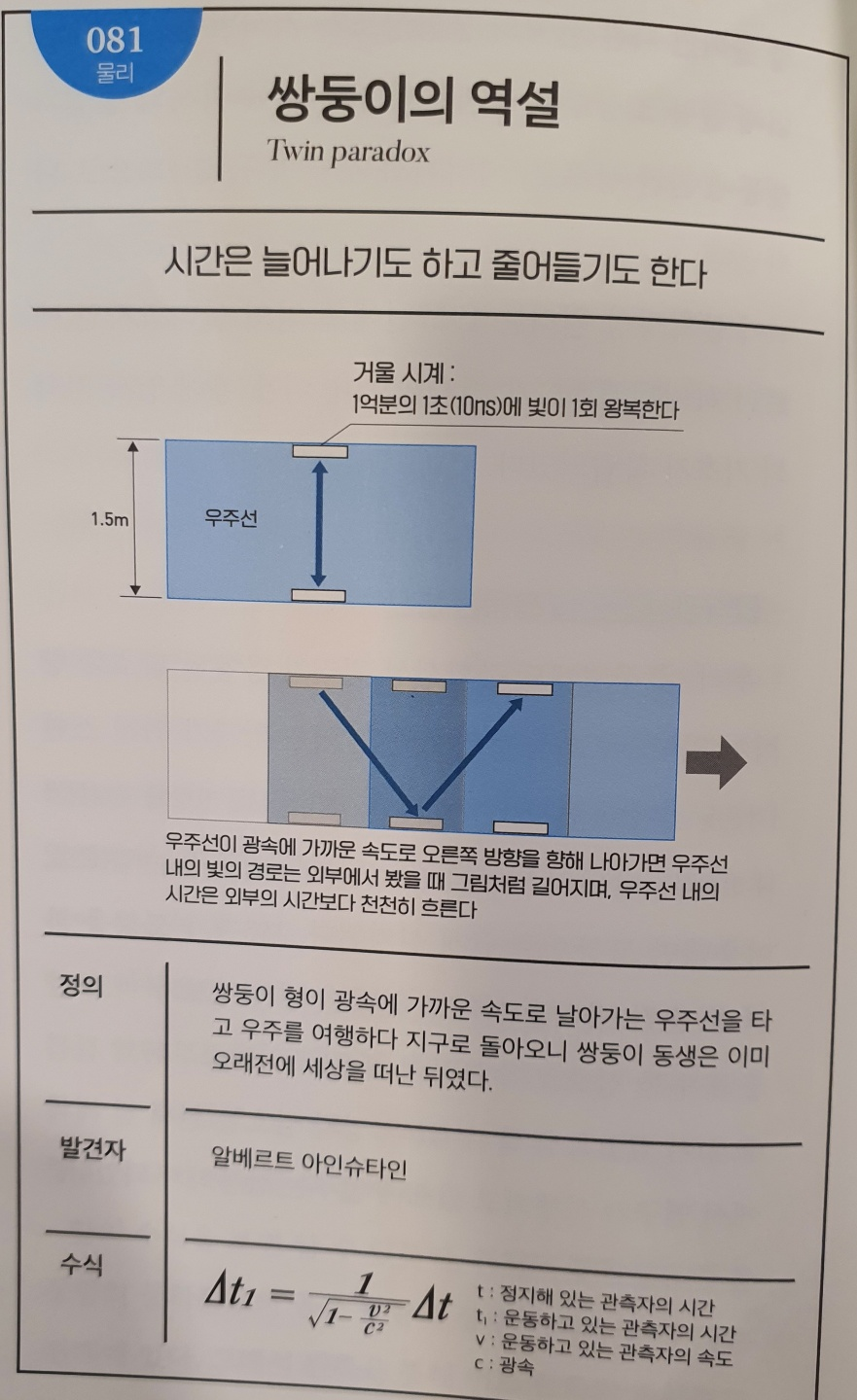
No.081 쌍둥이의 역설
No.082 훅의 법칙
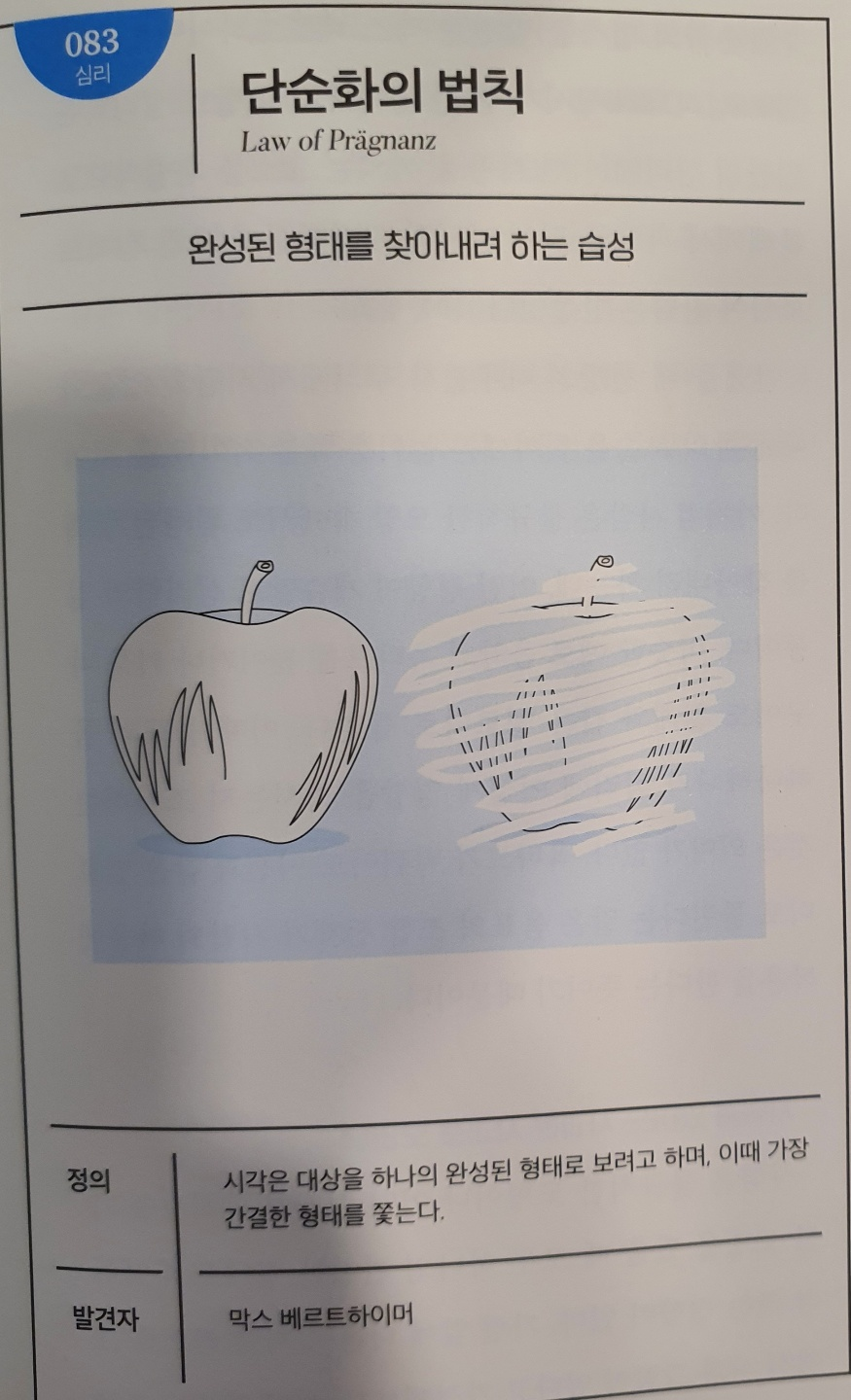
No.083 단순화의 법칙
Part. 4
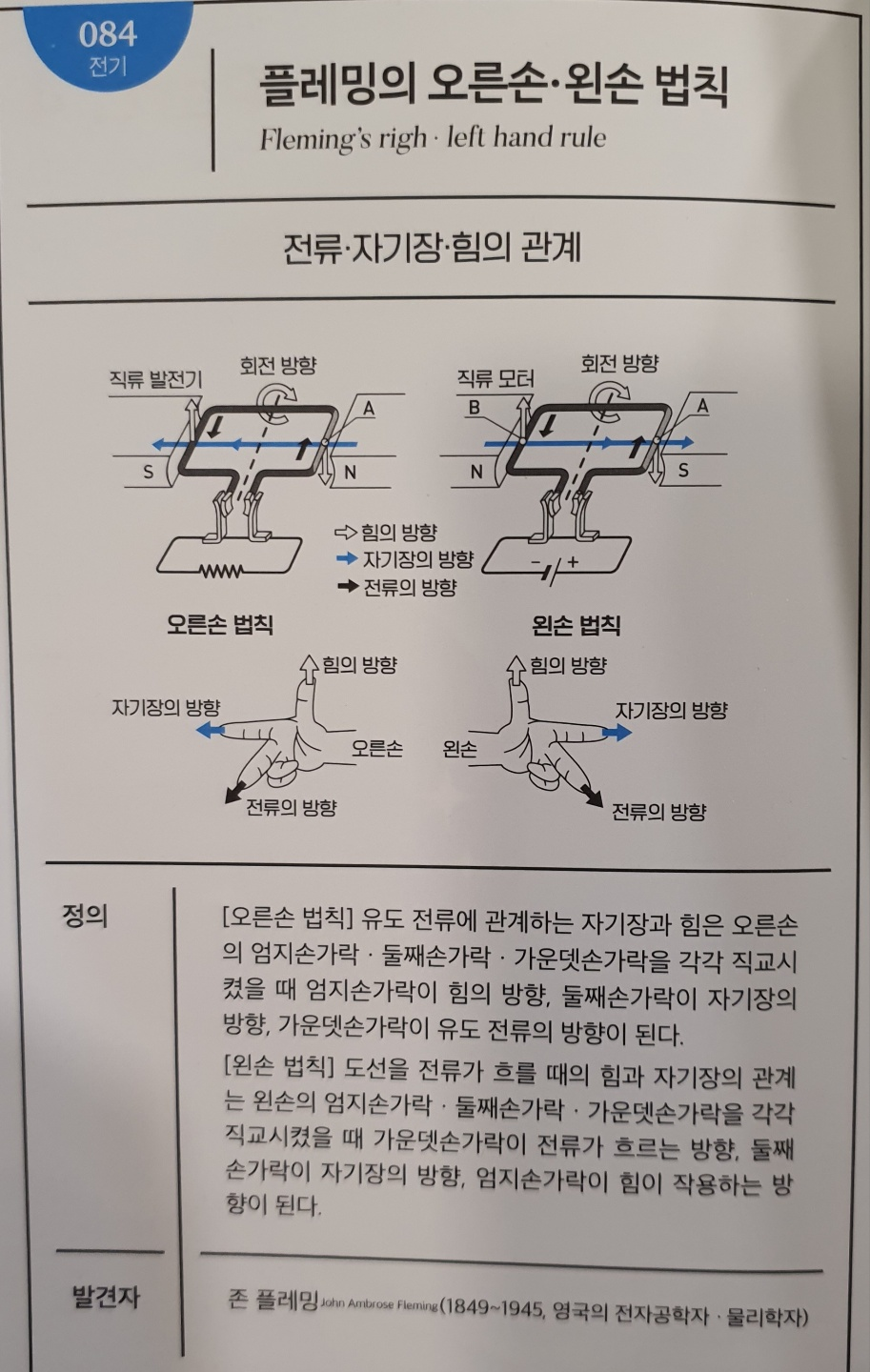
No.084 플레밍의 오른손·왼손 법칙
No.085 헵의 법칙
No.086 페티-클라크의 법칙
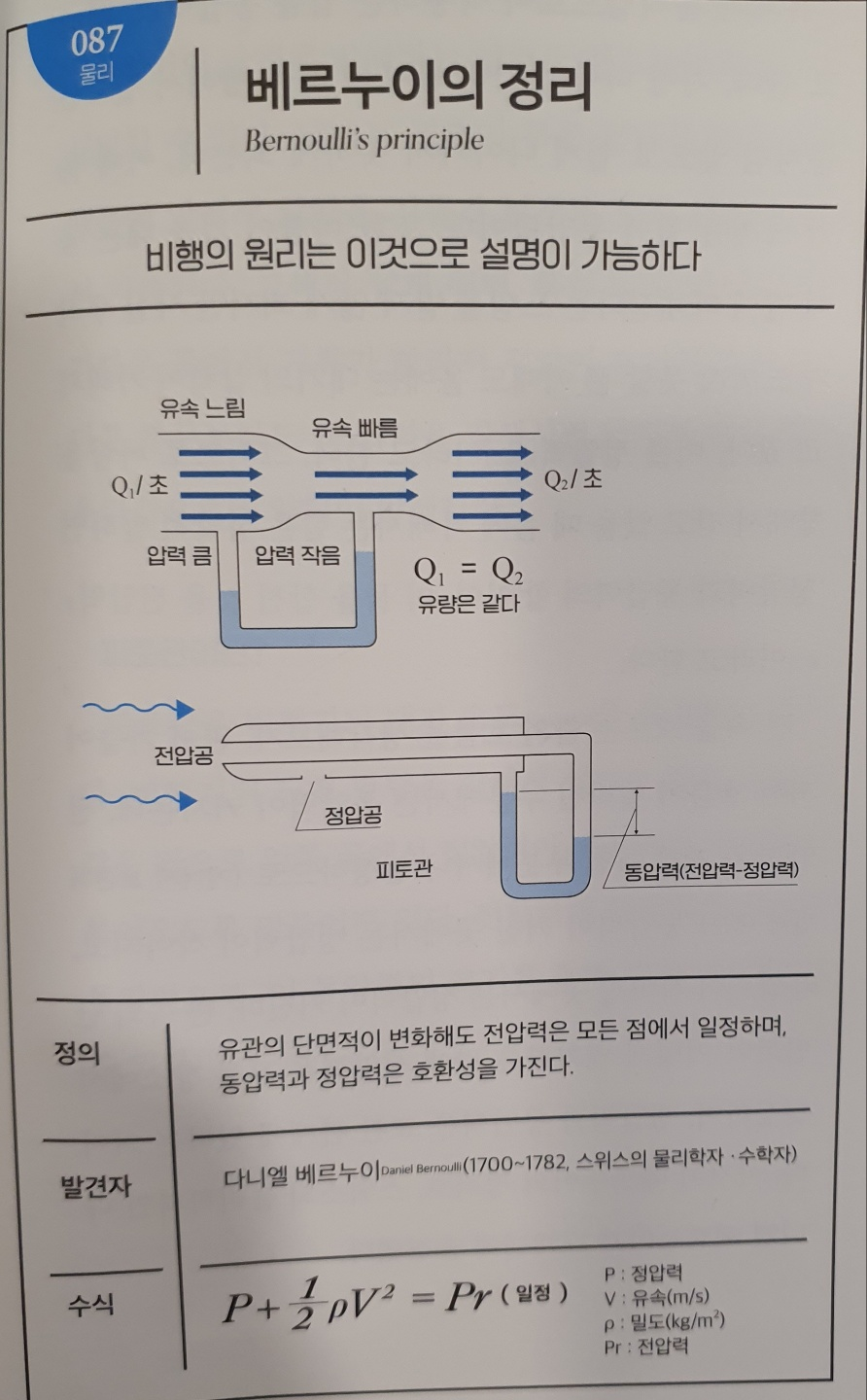
No.087 베르누이의 정리
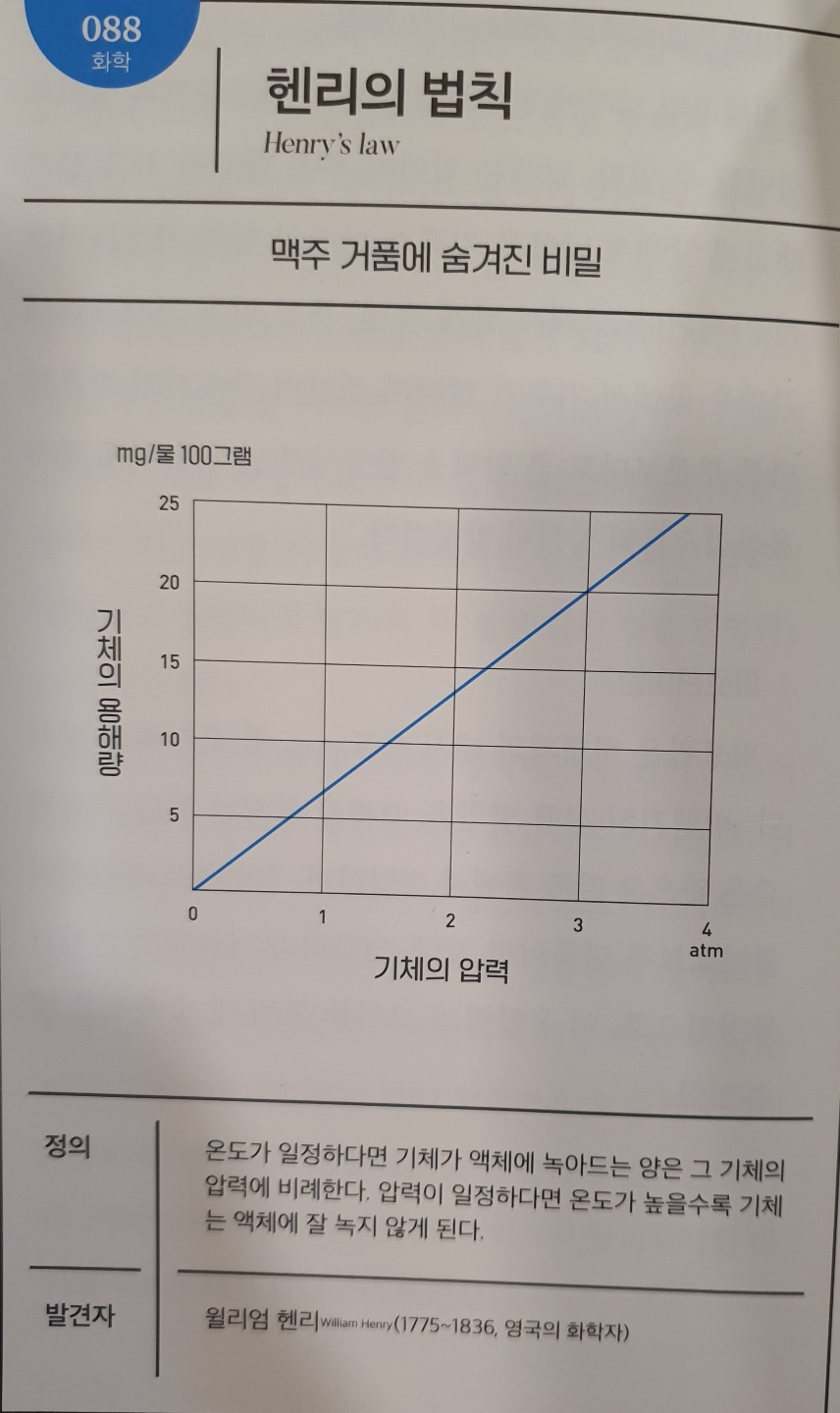
No.088 헨리의 법칙
No.089 바위스 발롯의 법칙
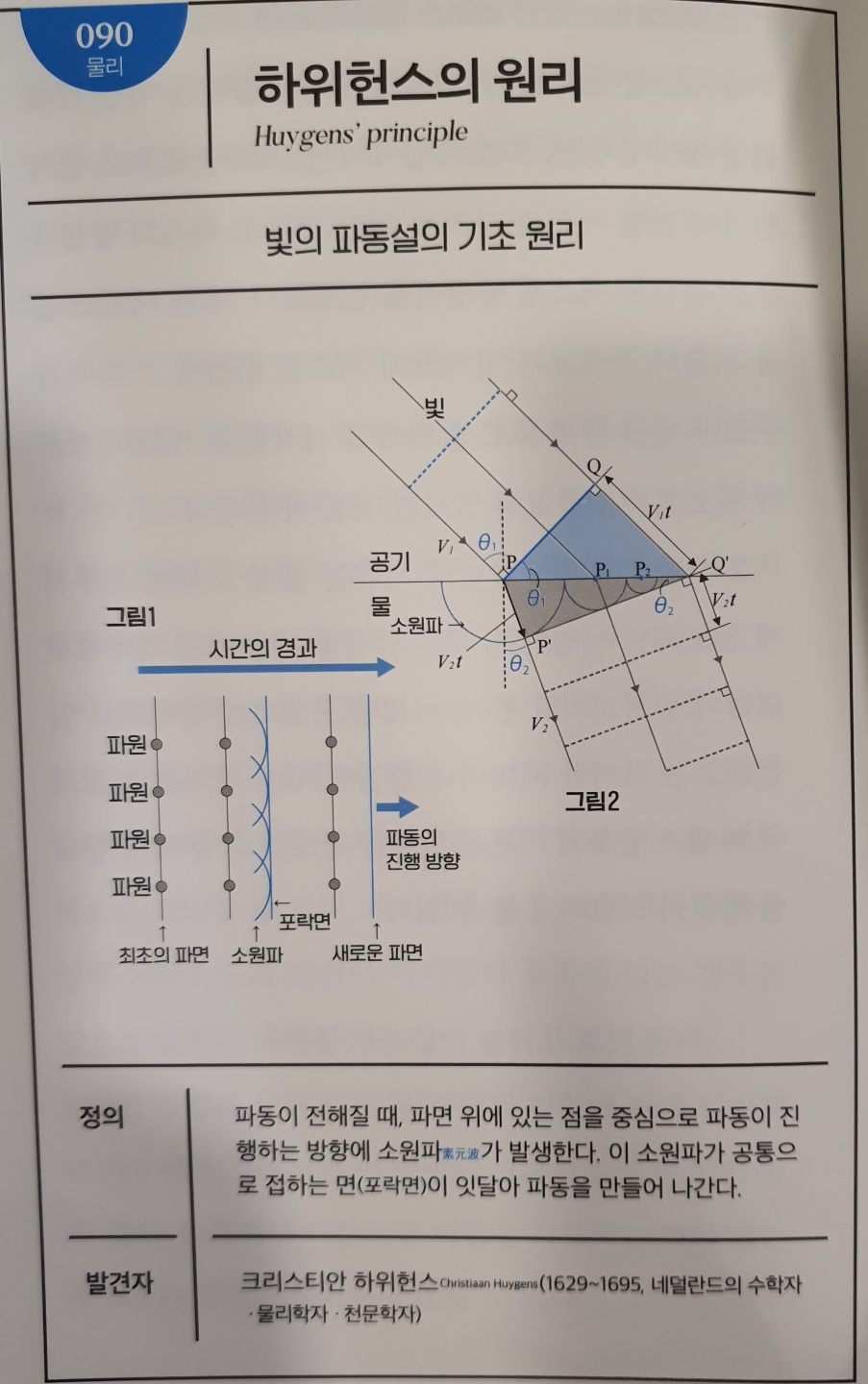
No.090 하위헌스의 원리
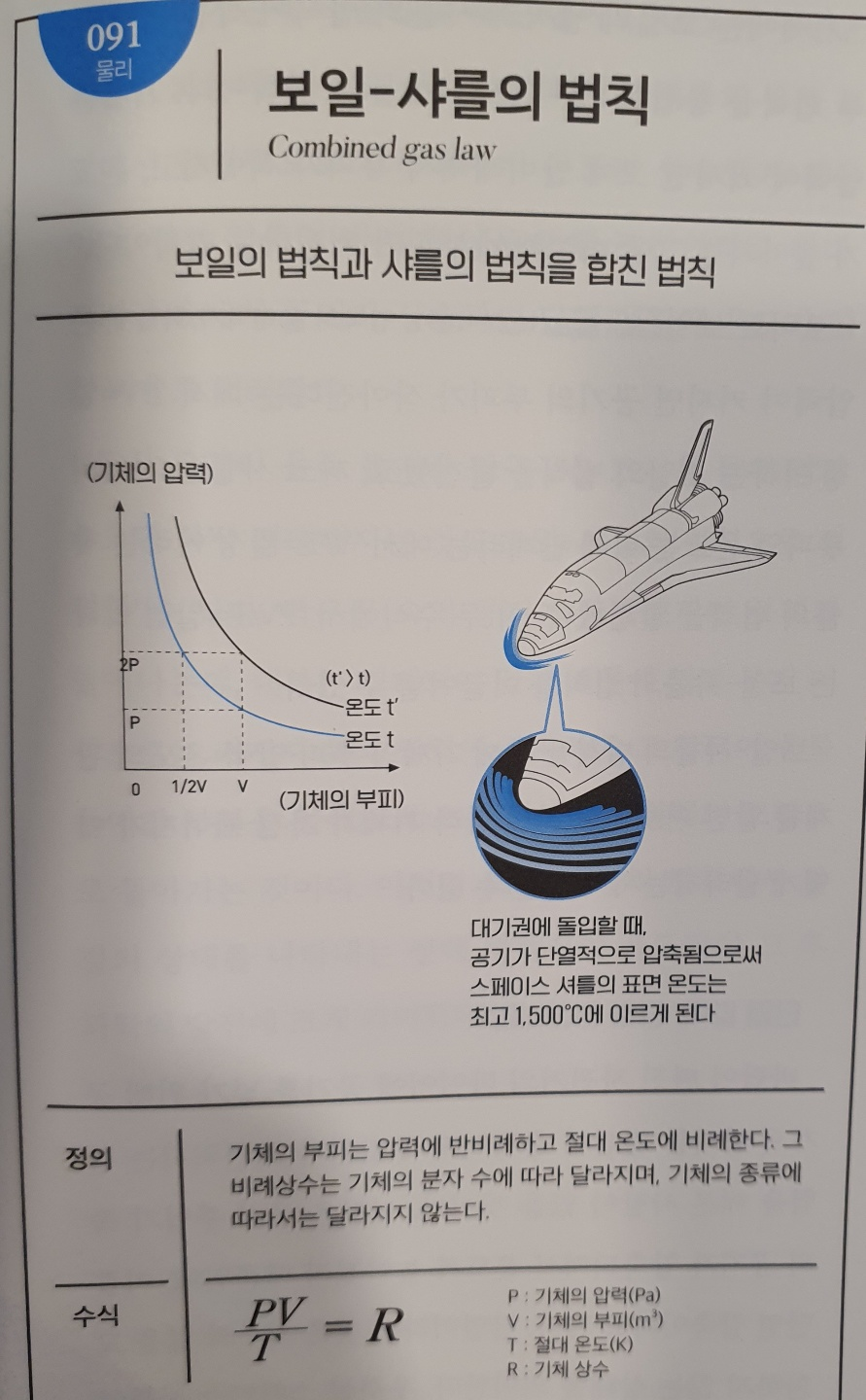
No.091 보일-샤를의 법칙
No.092 보일의 법칙
No.093 보데의 법칙
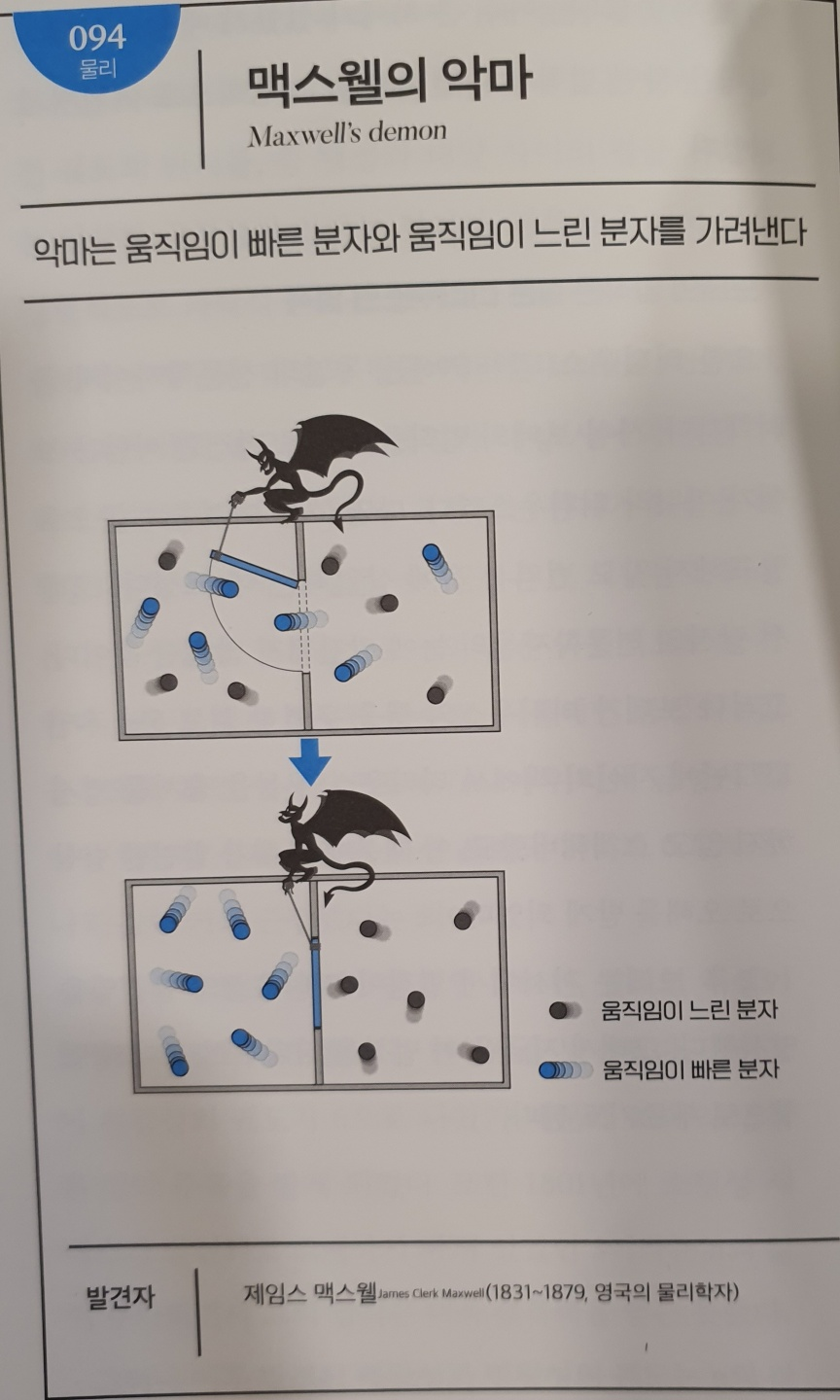
No.094 맥스웰의 악마
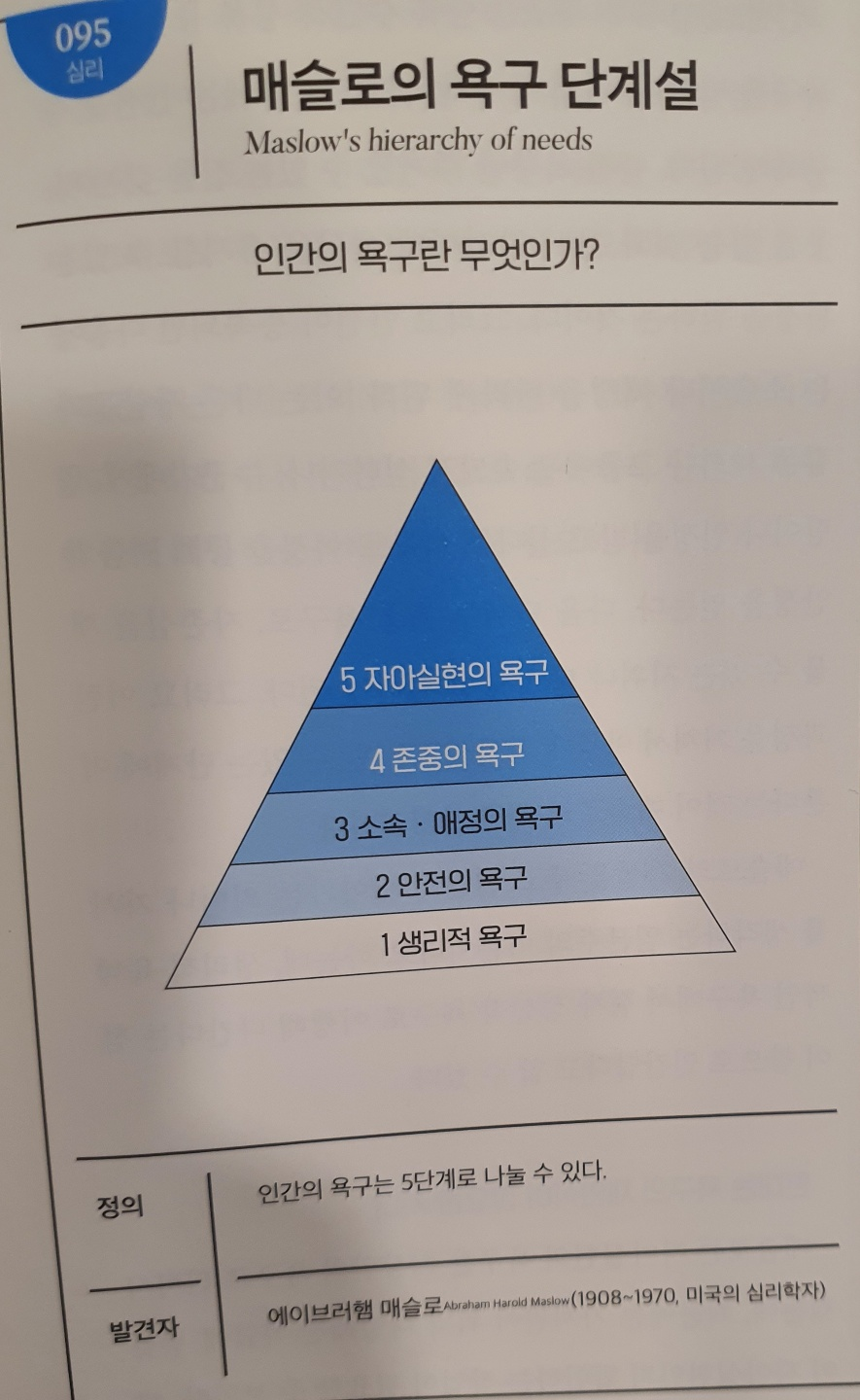
No.095 매슬로의 욕구 단계설
No.096 무어의 법칙
No.097 머레이비언의 법칙
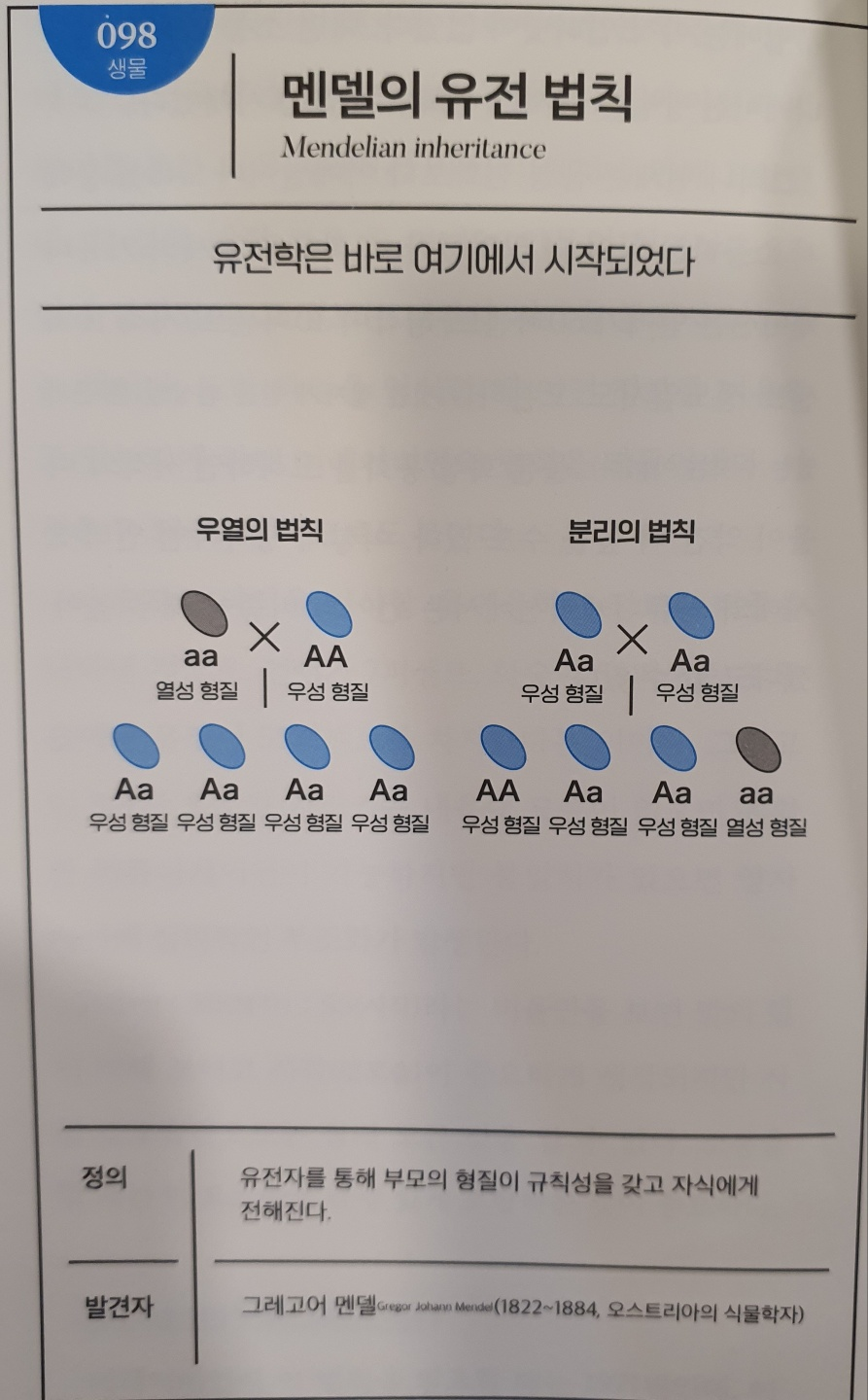
No.098 멘델의 유전 법칙
No.099 모즐리의 법칙
No.100 라플라스의 악마
No.101 란체스터의 법칙
No.102 리코의 법칙
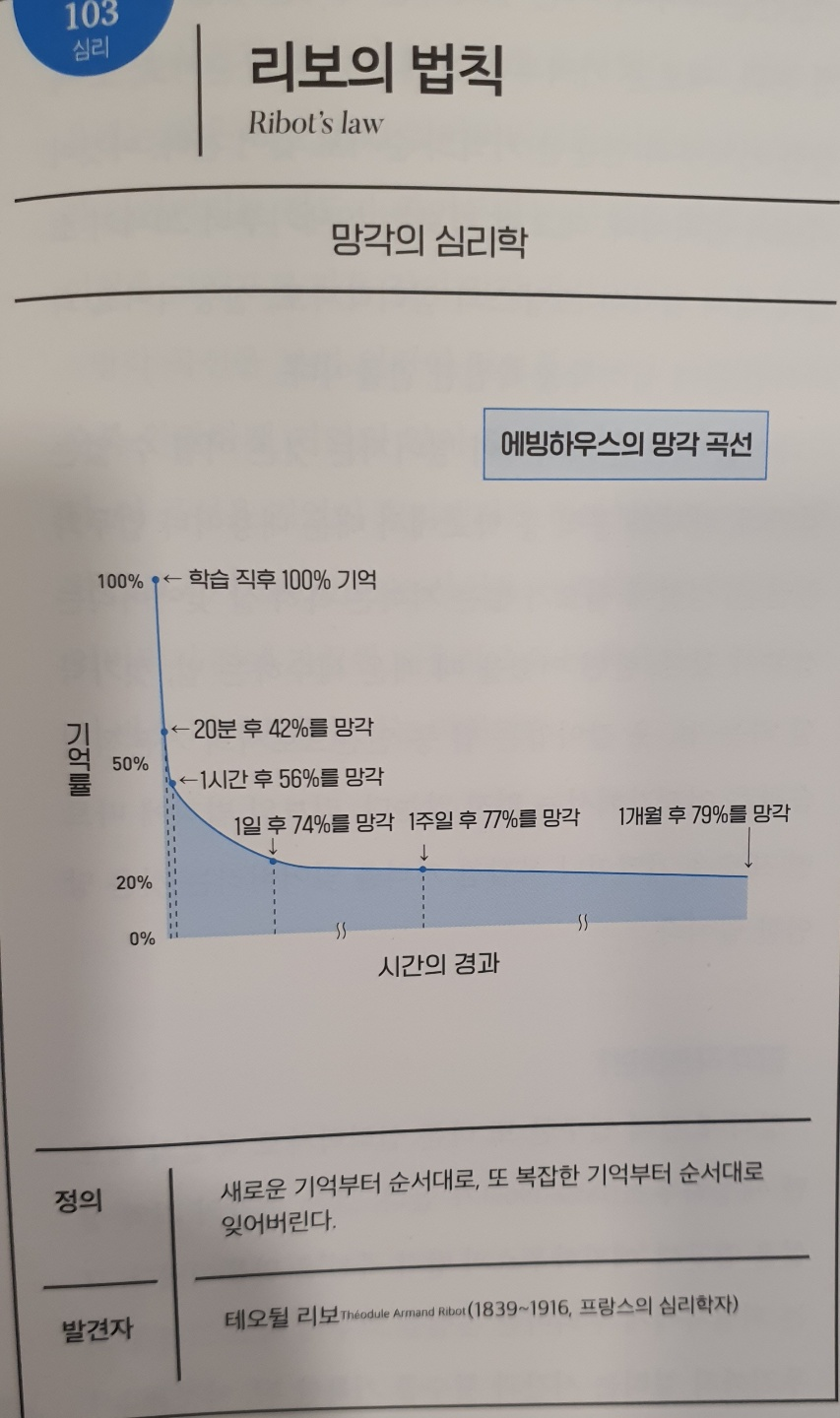
No.103 리보의 법칙
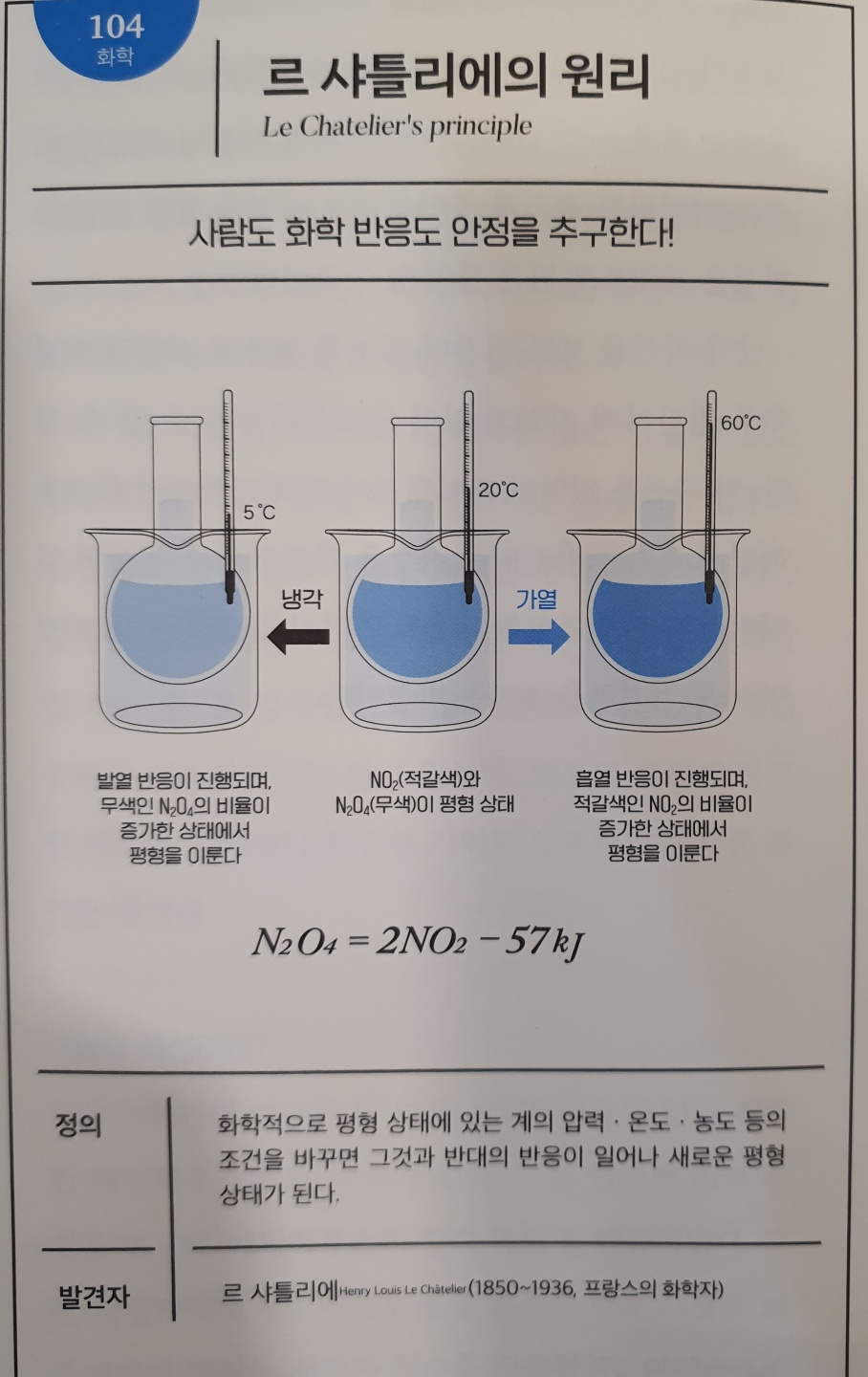
No.104 르 샤틀리에의 원리
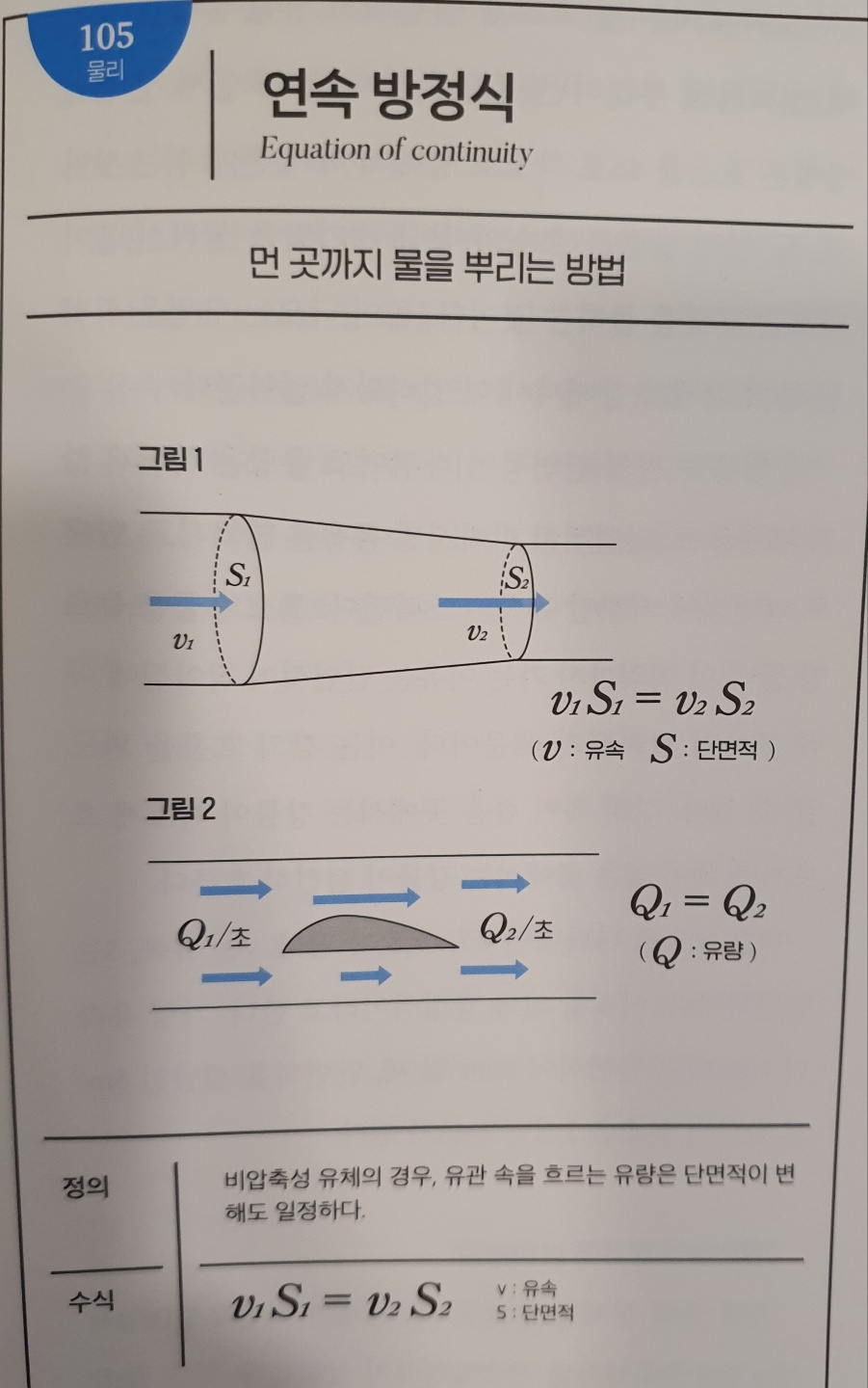
No.105 연속 방정식
'읽기' 카테고리의 다른 글
| 진화와 창의성 / 안드레아스 바그너 (0) | 2022.07.19 |
|---|---|
| 팬데믹 다음 세상을 위한 텐 레슨 / 파리드 자카리아 (0) | 2022.07.19 |
| 거의 모든 물질의 화학 / 김병민 (0) | 2022.07.15 |
| 원시유교 / 한성구 (0) | 2022.07.15 |
| 관념의 모험 / 화이트헤드 (0) | 2022.07.15 |
